tests_exhaustive.c File Reference

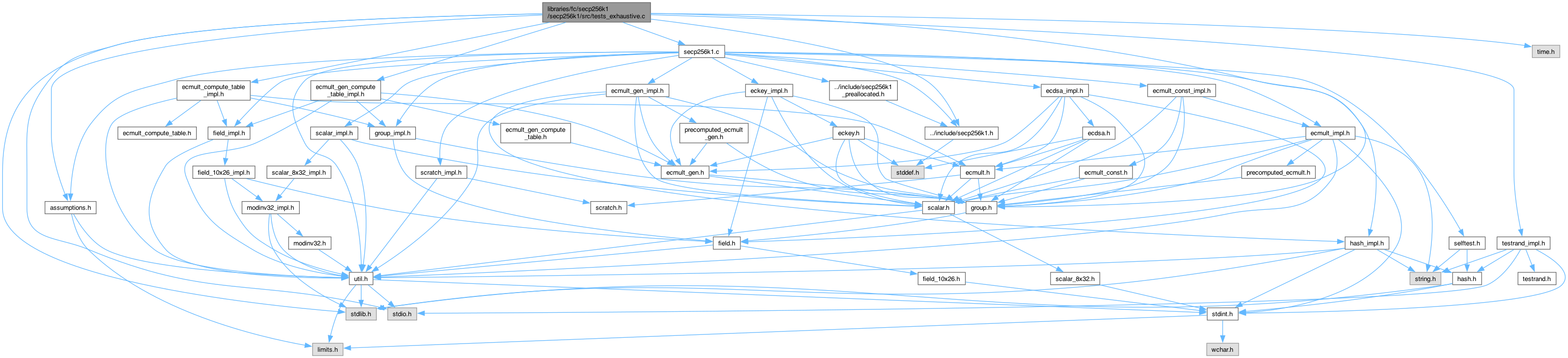
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "secp256k1.c"
#include "../include/secp256k1.h"
#include "assumptions.h"
#include "group.h"
#include "testrand_impl.h"
#include "ecmult_compute_table_impl.h"
#include "ecmult_gen_compute_table_impl.h"

Include dependency graph for tests_exhaustive.c:

Go to the source code of this file.

Classes
struct	ecmult_multi_data

Macros
#define	EXHAUSTIVE_TEST_ORDER   13

Functions
void	ge_equals_ge (const secp256k1_ge *a, const secp256k1_ge *b)
void	ge_equals_gej (const secp256k1_ge *a, const secp256k1_gej *b)
void	random_fe (secp256k1_fe *x)
int	secp256k1_nonce_function_smallint (unsigned char *nonce32, const unsigned char *msg32, const unsigned char *key32, const unsigned char *algo16, void *data, unsigned int attempt)
void	test_exhaustive_endomorphism (const secp256k1_ge *group)
void	test_exhaustive_addition (const secp256k1_ge *group, const secp256k1_gej *groupj)
void	test_exhaustive_ecmult (const secp256k1_ge *group, const secp256k1_gej *groupj)
void	test_exhaustive_ecmult_multi (const secp256k1_context *ctx, const secp256k1_ge *group)
void	r_from_k (secp256k1_scalar *r, const secp256k1_ge *group, int k, int *overflow)
void	test_exhaustive_verify (const secp256k1_context *ctx, const secp256k1_ge *group)
void	test_exhaustive_sign (const secp256k1_context *ctx, const secp256k1_ge *group)
int	main (int argc, char **argv)

Macro Definition Documentation

EXHAUSTIVE_TEST_ORDER

#define EXHAUSTIVE_TEST_ORDER   13

Definition at line 17 of file tests_exhaustive.c.

Function Documentation

ge_equals_ge()

void ge_equals_ge	(	const secp256k1_ge *	a,
		const secp256k1_ge *	b )

stolen from tests.c

Definition at line 31 of file tests_exhaustive.c.

                                                                {
    CHECK(a->infinity == b->infinity);
    if (a->infinity) {
        return;
    }
    CHECK(secp256k1_fe_equal_var(&a->x, &b->x));
    CHECK(secp256k1_fe_equal_var(&a->y, &b->y));
}

Here is the caller graph for this function:

ge_equals_gej()

void ge_equals_gej	(	const secp256k1_ge *	a,
		const secp256k1_gej *	b )

Definition at line 40 of file tests_exhaustive.c.

                                                                  {
    secp256k1_fe z2s;
    secp256k1_fe u1, u2, s1, s2;
    CHECK(a->infinity == b->infinity);
    if (a->infinity) {
        return;
    }
    /* Check a.x * b.z^2 == b.x && a.y * b.z^3 == b.y, to avoid inverses. */
    secp256k1_fe_sqr(&z2s, &b->z);
    secp256k1_fe_mul(&u1, &a->x, &z2s);
    u2 = b->x; secp256k1_fe_normalize_weak(&u2);
    secp256k1_fe_mul(&s1, &a->y, &z2s); secp256k1_fe_mul(&s1, &s1, &b->z);
    s2 = b->y; secp256k1_fe_normalize_weak(&s2);
    CHECK(secp256k1_fe_equal_var(&u1, &u2));
    CHECK(secp256k1_fe_equal_var(&s1, &s2));
}

Here is the caller graph for this function:

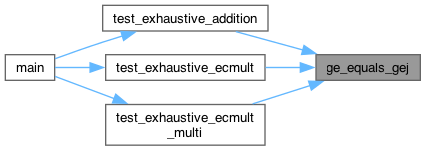
main()

int main	(	int	argc,
		char **	argv )

Definition at line 356 of file tests_exhaustive.c.

                                {
    int i;
    secp256k1_gej groupj[EXHAUSTIVE_TEST_ORDER];
    secp256k1_ge group[EXHAUSTIVE_TEST_ORDER];
    unsigned char rand32[32];
    secp256k1_context *ctx;
 
    /* Disable buffering for stdout to improve reliability of getting
     * diagnostic information. Happens right at the start of main because
     * setbuf must be used before any other operation on the stream. */
    setbuf(stdout, NULL);
    /* Also disable buffering for stderr because it's not guaranteed that it's
     * unbuffered on all systems. */
    setbuf(stderr, NULL);
 
    printf("Exhaustive tests for order %lu\n", (unsigned long)EXHAUSTIVE_TEST_ORDER);
 
    /* find iteration count */
    if (argc > 1) {
        count = strtol(argv[1], NULL, 0);
    }
    printf("test count = %i\n", count);
 
    /* find random seed */
    secp256k1_testrand_init(argc > 2 ? argv[2] : NULL);
 
    /* set up split processing */
    if (argc > 4) {
        num_cores = strtol(argv[3], NULL, 0);
        this_core = strtol(argv[4], NULL, 0);
        if (num_cores < 1 || this_core >= num_cores) {
            fprintf(stderr, "Usage: %s [count] [seed] [numcores] [thiscore]\n", argv[0]);
            return 1;
        }
        printf("running tests for core %lu (out of [0..%lu])\n", (unsigned long)this_core, (unsigned long)num_cores - 1);
    }
 
    /* Recreate the ecmult{,_gen} tables using the right generator (as selected via EXHAUSTIVE_TEST_ORDER) */
    secp256k1_ecmult_gen_compute_table(&secp256k1_ecmult_gen_prec_table[0][0], &secp256k1_ge_const_g, ECMULT_GEN_PREC_BITS);
    secp256k1_ecmult_compute_two_tables(secp256k1_pre_g, secp256k1_pre_g_128, WINDOW_G, &secp256k1_ge_const_g);
 
    while (count--) {
        /* Build context */
        ctx = secp256k1_context_create(SECP256K1_CONTEXT_SIGN | SECP256K1_CONTEXT_VERIFY);
        secp256k1_testrand256(rand32);
        CHECK(secp256k1_context_randomize(ctx, rand32));
 
        /* Generate the entire group */
        secp256k1_gej_set_infinity(&groupj[0]);
        secp256k1_ge_set_gej(&group[0], &groupj[0]);
        for (i = 1; i < EXHAUSTIVE_TEST_ORDER; i++) {
            secp256k1_gej_add_ge(&groupj[i], &groupj[i - 1], &secp256k1_ge_const_g);
            secp256k1_ge_set_gej(&group[i], &groupj[i]);
            if (count != 0) {
                /* Set a different random z-value for each Jacobian point, except z=1
                   is used in the last iteration. */
                secp256k1_fe z;
                random_fe(&z);
                secp256k1_gej_rescale(&groupj[i], &z);
            }
 
            /* Verify against ecmult_gen */
            {
                secp256k1_scalar scalar_i;
                secp256k1_gej generatedj;
                secp256k1_ge generated;
 
                secp256k1_scalar_set_int(&scalar_i, i);
                secp256k1_ecmult_gen(&ctx->ecmult_gen_ctx, &generatedj, &scalar_i);
                secp256k1_ge_set_gej(&generated, &generatedj);
 
                CHECK(group[i].infinity == 0);
                CHECK(generated.infinity == 0);
                CHECK(secp256k1_fe_equal_var(&generated.x, &group[i].x));
                CHECK(secp256k1_fe_equal_var(&generated.y, &group[i].y));
            }
        }
 
        /* Run the tests */
        test_exhaustive_endomorphism(group);
        test_exhaustive_addition(group, groupj);
        test_exhaustive_ecmult(group, groupj);
        test_exhaustive_ecmult_multi(ctx, group);
        test_exhaustive_sign(ctx, group);
        test_exhaustive_verify(ctx, group);
 
#ifdef ENABLE_MODULE_RECOVERY
        test_exhaustive_recovery(ctx, group);
#endif
#ifdef ENABLE_MODULE_EXTRAKEYS
        test_exhaustive_extrakeys(ctx, group);
#endif
#ifdef ENABLE_MODULE_SCHNORRSIG
        test_exhaustive_schnorrsig(ctx);
#endif
 
        secp256k1_context_destroy(ctx);
    }
 
    secp256k1_testrand_finish();
 
    printf("no problems found\n");
    return 0;
}

Here is the call graph for this function:

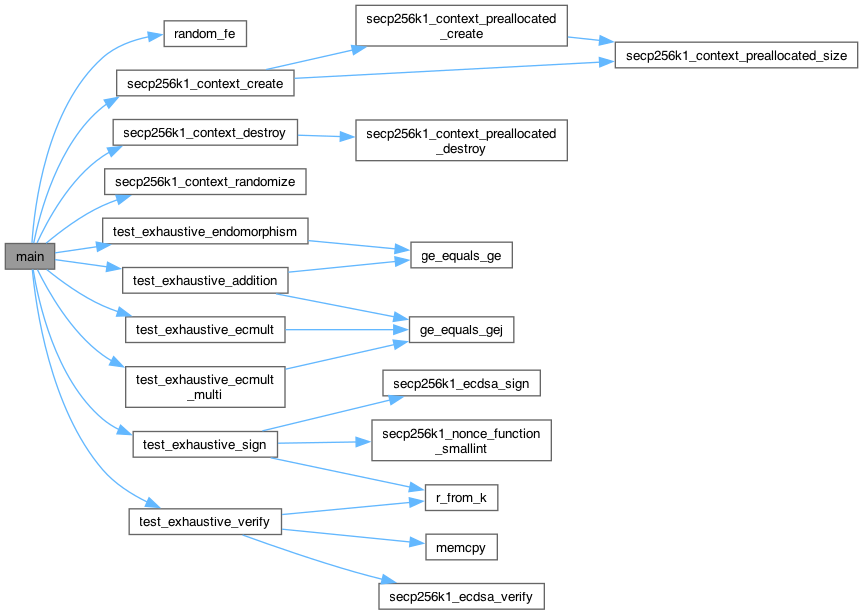
r_from_k()

void r_from_k	(	secp256k1_scalar *	r,
		const secp256k1_ge *	group,
		int	k,
		int *	overflow )

Definition at line 232 of file tests_exhaustive.c.

                                                                                    {
    secp256k1_fe x;
    unsigned char x_bin[32];
    k %= EXHAUSTIVE_TEST_ORDER;
    x = group[k].x;
    secp256k1_fe_normalize(&x);
    secp256k1_fe_get_b32(x_bin, &x);
    secp256k1_scalar_set_b32(r, x_bin, overflow);
}

Here is the caller graph for this function:

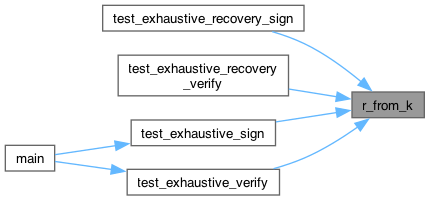
random_fe()

void random_fe

(

secp256k1_fe *

x

)

Definition at line 57 of file tests_exhaustive.c.

                                {
    unsigned char bin[32];
    do {
        secp256k1_testrand256(bin);
        if (secp256k1_fe_set_b32(x, bin)) {
            return;
        }
    } while(1);
}

Here is the caller graph for this function:

secp256k1_nonce_function_smallint()

int secp256k1_nonce_function_smallint	(	unsigned char *	nonce32,
		const unsigned char *	msg32,
		const unsigned char *	key32,
		const unsigned char *	algo16,
		void *	data,
		unsigned int	attempt )

Definition at line 77 of file tests_exhaustive.c.

                                                                        {
    secp256k1_scalar s;
    int *idata = data;
    (void)msg32;
    (void)key32;
    (void)algo16;
    /* Some nonces cannot be used because they'd cause s and/or r to be zero.
     * The signing function has retry logic here that just re-calls the nonce
     * function with an increased `attempt`. So if attempt > 0 this means we
     * need to change the nonce to avoid an infinite loop. */
    if (attempt > 0) {
        *idata = (*idata + 1) % EXHAUSTIVE_TEST_ORDER;
    }
    secp256k1_scalar_set_int(&s, *idata);
    secp256k1_scalar_get_b32(nonce32, &s);
    return 1;
}

Here is the caller graph for this function:

test_exhaustive_addition()

void test_exhaustive_addition	(	const secp256k1_ge *	group,
		const secp256k1_gej *	groupj )

Definition at line 106 of file tests_exhaustive.c.

                                                                                      {
    int i, j;
    uint64_t iter = 0;
 
    /* Sanity-check (and check infinity functions) */
    CHECK(secp256k1_ge_is_infinity(&group[0]));
    CHECK(secp256k1_gej_is_infinity(&groupj[0]));
    for (i = 1; i < EXHAUSTIVE_TEST_ORDER; i++) {
        CHECK(!secp256k1_ge_is_infinity(&group[i]));
        CHECK(!secp256k1_gej_is_infinity(&groupj[i]));
    }
 
    /* Check all addition formulae */
    for (j = 0; j < EXHAUSTIVE_TEST_ORDER; j++) {
        secp256k1_fe fe_inv;
        if (skip_section(&iter)) continue;
        secp256k1_fe_inv(&fe_inv, &groupj[j].z);
        for (i = 0; i < EXHAUSTIVE_TEST_ORDER; i++) {
            secp256k1_ge zless_gej;
            secp256k1_gej tmp;
            /* add_var */
            secp256k1_gej_add_var(&tmp, &groupj[i], &groupj[j], NULL);
            ge_equals_gej(&group[(i + j) % EXHAUSTIVE_TEST_ORDER], &tmp);
            /* add_ge */
            if (j > 0) {
                secp256k1_gej_add_ge(&tmp, &groupj[i], &group[j]);
                ge_equals_gej(&group[(i + j) % EXHAUSTIVE_TEST_ORDER], &tmp);
            }
            /* add_ge_var */
            secp256k1_gej_add_ge_var(&tmp, &groupj[i], &group[j], NULL);
            ge_equals_gej(&group[(i + j) % EXHAUSTIVE_TEST_ORDER], &tmp);
            /* add_zinv_var */
            zless_gej.infinity = groupj[j].infinity;
            zless_gej.x = groupj[j].x;
            zless_gej.y = groupj[j].y;
            secp256k1_gej_add_zinv_var(&tmp, &groupj[i], &zless_gej, &fe_inv);
            ge_equals_gej(&group[(i + j) % EXHAUSTIVE_TEST_ORDER], &tmp);
        }
    }
 
    /* Check doubling */
    for (i = 0; i < EXHAUSTIVE_TEST_ORDER; i++) {
        secp256k1_gej tmp;
        secp256k1_gej_double(&tmp, &groupj[i]);
        ge_equals_gej(&group[(2 * i) % EXHAUSTIVE_TEST_ORDER], &tmp);
        secp256k1_gej_double_var(&tmp, &groupj[i], NULL);
        ge_equals_gej(&group[(2 * i) % EXHAUSTIVE_TEST_ORDER], &tmp);
    }
 
    /* Check negation */
    for (i = 1; i < EXHAUSTIVE_TEST_ORDER; i++) {
        secp256k1_ge tmp;
        secp256k1_gej tmpj;
        secp256k1_ge_neg(&tmp, &group[i]);
        ge_equals_ge(&group[EXHAUSTIVE_TEST_ORDER - i], &tmp);
        secp256k1_gej_neg(&tmpj, &groupj[i]);
        ge_equals_gej(&group[EXHAUSTIVE_TEST_ORDER - i], &tmpj);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

test_exhaustive_ecmult()

void test_exhaustive_ecmult	(	const secp256k1_ge *	group,
		const secp256k1_gej *	groupj )

Definition at line 166 of file tests_exhaustive.c.

                                                                                    {
    int i, j, r_log;
    uint64_t iter = 0;
    for (r_log = 1; r_log < EXHAUSTIVE_TEST_ORDER; r_log++) {
        for (j = 0; j < EXHAUSTIVE_TEST_ORDER; j++) {
            if (skip_section(&iter)) continue;
            for (i = 0; i < EXHAUSTIVE_TEST_ORDER; i++) {
                secp256k1_gej tmp;
                secp256k1_scalar na, ng;
                secp256k1_scalar_set_int(&na, i);
                secp256k1_scalar_set_int(&ng, j);
 
                secp256k1_ecmult(&tmp, &groupj[r_log], &na, &ng);
                ge_equals_gej(&group[(i * r_log + j) % EXHAUSTIVE_TEST_ORDER], &tmp);
 
                if (i > 0) {
                    secp256k1_ecmult_const(&tmp, &group[i], &ng, 256);
                    ge_equals_gej(&group[(i * j) % EXHAUSTIVE_TEST_ORDER], &tmp);
                }
            }
        }
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

test_exhaustive_ecmult_multi()

void test_exhaustive_ecmult_multi	(	const secp256k1_context *	ctx,
		const secp256k1_ge *	group )

Definition at line 202 of file tests_exhaustive.c.

                                                                                           {
    int i, j, k, x, y;
    uint64_t iter = 0;
    secp256k1_scratch *scratch = secp256k1_scratch_create(&ctx->error_callback, 4096);
    for (i = 0; i < EXHAUSTIVE_TEST_ORDER; i++) {
        for (j = 0; j < EXHAUSTIVE_TEST_ORDER; j++) {
            for (k = 0; k < EXHAUSTIVE_TEST_ORDER; k++) {
                for (x = 0; x < EXHAUSTIVE_TEST_ORDER; x++) {
                    if (skip_section(&iter)) continue;
                    for (y = 0; y < EXHAUSTIVE_TEST_ORDER; y++) {
                        secp256k1_gej tmp;
                        secp256k1_scalar g_sc;
                        ecmult_multi_data data;
 
                        secp256k1_scalar_set_int(&data.sc[0], i);
                        secp256k1_scalar_set_int(&data.sc[1], j);
                        secp256k1_scalar_set_int(&g_sc, k);
                        data.pt[0] = group[x];
                        data.pt[1] = group[y];
 
                        secp256k1_ecmult_multi_var(&ctx->error_callback, scratch, &tmp, &g_sc, ecmult_multi_callback, &data, 2);
                        ge_equals_gej(&group[(i * x + j * y + k) % EXHAUSTIVE_TEST_ORDER], &tmp);
                    }
                }
            }
        }
    }
    secp256k1_scratch_destroy(&ctx->error_callback, scratch);
}

Here is the call graph for this function:

Here is the caller graph for this function:

test_exhaustive_endomorphism()

void test_exhaustive_endomorphism

(

const secp256k1_ge *

group

)

Definition at line 97 of file tests_exhaustive.c.

                                                             {
    int i;
    for (i = 0; i < EXHAUSTIVE_TEST_ORDER; i++) {
        secp256k1_ge res;
        secp256k1_ge_mul_lambda(&res, &group[i]);
        ge_equals_ge(&group[i * EXHAUSTIVE_TEST_LAMBDA % EXHAUSTIVE_TEST_ORDER], &res);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

test_exhaustive_sign()

void test_exhaustive_sign	(	const secp256k1_context *	ctx,
		const secp256k1_ge *	group )

Definition at line 295 of file tests_exhaustive.c.

                                                                                   {
    int i, j, k;
    uint64_t iter = 0;
 
    /* Loop */
    for (i = 1; i < EXHAUSTIVE_TEST_ORDER; i++) {  /* message */
        for (j = 1; j < EXHAUSTIVE_TEST_ORDER; j++) {  /* key */
            if (skip_section(&iter)) continue;
            for (k = 1; k < EXHAUSTIVE_TEST_ORDER; k++) {  /* nonce */
                const int starting_k = k;
                int ret;
                secp256k1_ecdsa_signature sig;
                secp256k1_scalar sk, msg, r, s, expected_r;
                unsigned char sk32[32], msg32[32];
                secp256k1_scalar_set_int(&msg, i);
                secp256k1_scalar_set_int(&sk, j);
                secp256k1_scalar_get_b32(sk32, &sk);
                secp256k1_scalar_get_b32(msg32, &msg);
 
                ret = secp256k1_ecdsa_sign(ctx, &sig, msg32, sk32, secp256k1_nonce_function_smallint, &k);
                CHECK(ret == 1);
 
                secp256k1_ecdsa_signature_load(ctx, &r, &s, &sig);
                /* Note that we compute expected_r *after* signing -- this is important
                 * because our nonce-computing function function might change k during
                 * signing. */
                r_from_k(&expected_r, group, k, NULL);
                CHECK(r == expected_r);
                CHECK((k * s) % EXHAUSTIVE_TEST_ORDER == (i + r * j) % EXHAUSTIVE_TEST_ORDER ||
                      (k * (EXHAUSTIVE_TEST_ORDER - s)) % EXHAUSTIVE_TEST_ORDER == (i + r * j) % EXHAUSTIVE_TEST_ORDER);
 
                /* Overflow means we've tried every possible nonce */
                if (k < starting_k) {
                    break;
                }
            }
        }
    }
 
    /* We would like to verify zero-knowledge here by counting how often every
     * possible (s, r) tuple appears, but because the group order is larger
     * than the field order, when coercing the x-values to scalar values, some
     * appear more often than others, so we are actually not zero-knowledge.
     * (This effect also appears in the real code, but the difference is on the
     * order of 1/2^128th the field order, so the deviation is not useful to a
     * computationally bounded attacker.)
     */
}

Here is the call graph for this function:

Here is the caller graph for this function:

test_exhaustive_verify()

void test_exhaustive_verify	(	const secp256k1_context *	ctx,
		const secp256k1_ge *	group )

Definition at line 242 of file tests_exhaustive.c.

                                                                                     {
    int s, r, msg, key;
    uint64_t iter = 0;
    for (s = 1; s < EXHAUSTIVE_TEST_ORDER; s++) {
        for (r = 1; r < EXHAUSTIVE_TEST_ORDER; r++) {
            for (msg = 1; msg < EXHAUSTIVE_TEST_ORDER; msg++) {
                for (key = 1; key < EXHAUSTIVE_TEST_ORDER; key++) {
                    secp256k1_ge nonconst_ge;
                    secp256k1_ecdsa_signature sig;
                    secp256k1_pubkey pk;
                    secp256k1_scalar sk_s, msg_s, r_s, s_s;
                    secp256k1_scalar s_times_k_s, msg_plus_r_times_sk_s;
                    int k, should_verify;
                    unsigned char msg32[32];
 
                    if (skip_section(&iter)) continue;
 
                    secp256k1_scalar_set_int(&s_s, s);
                    secp256k1_scalar_set_int(&r_s, r);
                    secp256k1_scalar_set_int(&msg_s, msg);
                    secp256k1_scalar_set_int(&sk_s, key);
 
                    /* Verify by hand */
                    /* Run through every k value that gives us this r and check that *one* works.
                     * Note there could be none, there could be multiple, ECDSA is weird. */
                    should_verify = 0;
                    for (k = 0; k < EXHAUSTIVE_TEST_ORDER; k++) {
                        secp256k1_scalar check_x_s;
                        r_from_k(&check_x_s, group, k, NULL);
                        if (r_s == check_x_s) {
                            secp256k1_scalar_set_int(&s_times_k_s, k);
                            secp256k1_scalar_mul(&s_times_k_s, &s_times_k_s, &s_s);
                            secp256k1_scalar_mul(&msg_plus_r_times_sk_s, &r_s, &sk_s);
                            secp256k1_scalar_add(&msg_plus_r_times_sk_s, &msg_plus_r_times_sk_s, &msg_s);
                            should_verify |= secp256k1_scalar_eq(&s_times_k_s, &msg_plus_r_times_sk_s);
                        }
                    }
                    /* nb we have a "high s" rule */
                    should_verify &= !secp256k1_scalar_is_high(&s_s);
 
                    /* Verify by calling verify */
                    secp256k1_ecdsa_signature_save(&sig, &r_s, &s_s);
                    memcpy(&nonconst_ge, &group[sk_s], sizeof(nonconst_ge));
                    secp256k1_pubkey_save(&pk, &nonconst_ge);
                    secp256k1_scalar_get_b32(msg32, &msg_s);
                    CHECK(should_verify ==
                          secp256k1_ecdsa_verify(ctx, &sig, msg32, &pk));
                }
            }
        }
    }
}

Here is the call graph for this function:

Here is the caller graph for this function: