test_modular_arithmetic.cpp File Reference

#include <boost/test/included/unit_test.hpp>
#include <fc/exception/exception.hpp>
#include <fc/crypto/hex.hpp>
#include <fc/crypto/modular_arithmetic.hpp>
#include <fc/utility.hpp>
#include <chrono>
#include <random>
#include <limits>
#include "test_utils.hpp"

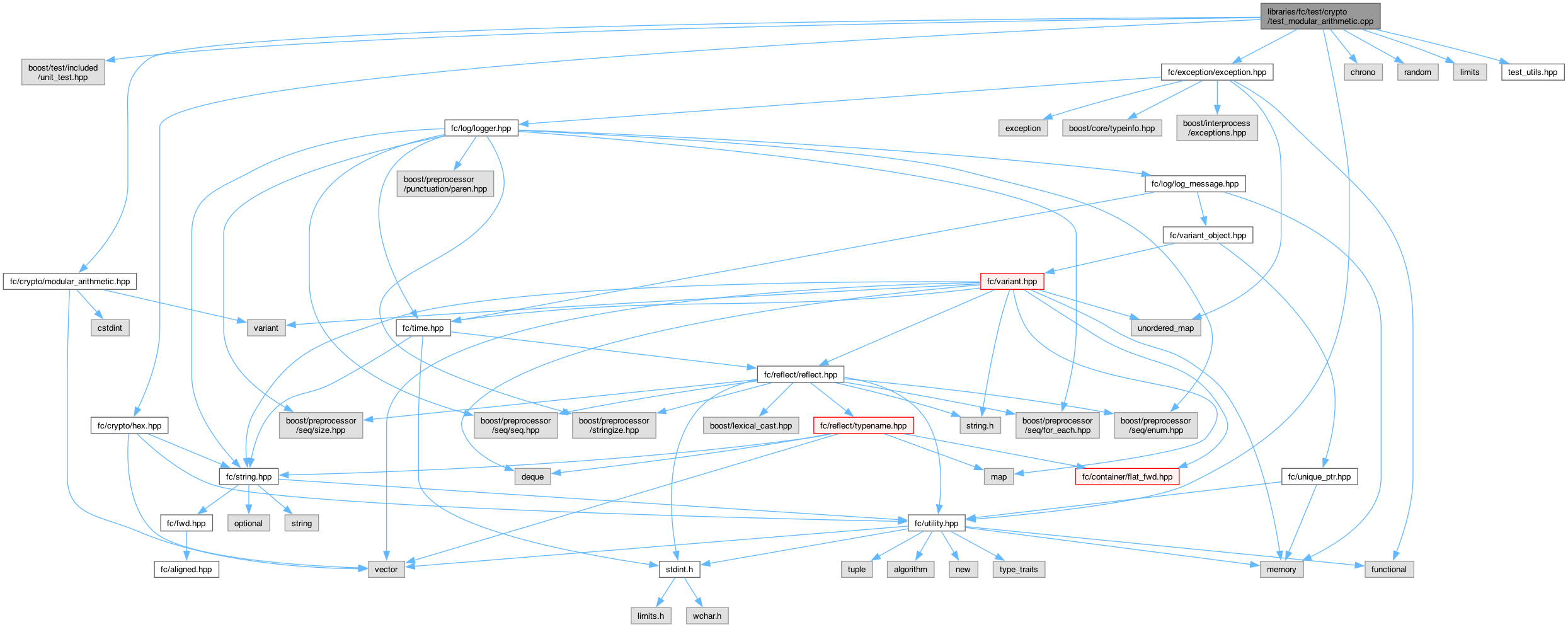
Include dependency graph for test_modular_arithmetic.cpp:

Go to the source code of this file.

Namespaces
namespace	std

Macros
#define	BOOST_TEST_MODULE   modular_arithmetic

Functions
std::ostream &	std::operator<< (std::ostream &st, const std::variant< fc::modular_arithmetic_error, bytes > &err)
	BOOST_AUTO_TEST_CASE (modexp)
	FC_LOG_AND_RETHROW ()
	BOOST_AUTO_TEST_CASE (modexp_benchmarking)

Macro Definition Documentation

BOOST_TEST_MODULE

#define BOOST_TEST_MODULE   modular_arithmetic

Definition at line 1 of file test_modular_arithmetic.cpp.

Function Documentation

BOOST_AUTO_TEST_CASE() [1/2]

BOOST_AUTO_TEST_CASE

(

modexp

)

Definition at line 30 of file test_modular_arithmetic.cpp.

                                 {
 
 
    using modexp_test = std::tuple<std::vector<string>, std::variant<fc::modular_arithmetic_error, bytes>>;
 
    const std::vector<modexp_test> tests {
        //test1
        {
            {
                "03",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2e",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f",
            },
            to_bytes("0000000000000000000000000000000000000000000000000000000000000001"),
        },
 
        //test2
        {
            {
                "",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2e",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f",
            },
            to_bytes("0000000000000000000000000000000000000000000000000000000000000000")
        },
 
        //test3
        {
            {
                "01",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2e",
                "",
            },
            modular_arithmetic_error::modulus_len_zero
        },
 
        //test4
        {
            {
                "01",
                "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2e",
                "0000",
            },
            to_bytes("0000")
        },
 
        //test5
        {
            {
                "00",
                "00",
                "0F",
            },
            to_bytes("01"),
        },
 
        //test6
        {
            {
                "00",
                "01",
                "0F",
            },
            to_bytes("00"),
        },
 
        //test7
        {
            {
                "01",
                "00",
                "0F",
            },
            to_bytes("01"),
        },
 
    };
 
    for(const auto& test : tests) {
        const auto& parts           = std::get<0>(test);
        const auto& expected_result = std::get<1>(test);
 
        auto base = to_bytes(parts[0]);
        auto exponent = to_bytes(parts[1]);
        auto modulus = to_bytes(parts[2]);
 
        auto res = fc::modexp(base, exponent, modulus);
        BOOST_CHECK_EQUAL(res, expected_result);
    }
 
} FC_LOG_AND_RETHROW();

Here is the call graph for this function:

BOOST_AUTO_TEST_CASE() [2/2]

BOOST_AUTO_TEST_CASE

(

modexp_benchmarking

)

Definition at line 122 of file test_modular_arithmetic.cpp.

                                              {
 
    std::mt19937 r(0x11223344);
 
    auto generate_random_bytes = [](std::mt19937& rand_eng, unsigned int num_bytes) {
        std::vector<char> result(num_bytes);
 
        uint_fast32_t v = 0;
        for(int byte_pos = 0, end = result.size(); byte_pos < end; ++byte_pos) {
            if ((byte_pos & 0x03) == 0) { // if divisible by 4
                v = rand_eng();
            }
            result[byte_pos] = v & 0xFF;
            v >>= 8;
        }
 
        return result;
    };
 
    static constexpr unsigned int num_trials = 10; // 10000
 
    static_assert(num_trials > 0);
 
    static constexpr unsigned int bit_calc_limit = 101; // 120
 
    static constexpr unsigned int start_num_bytes = 1;
    static constexpr unsigned int end_num_bytes   = 1 << ((bit_calc_limit + 7)/8);
 
    static_assert(start_num_bytes <= end_num_bytes);
 
    struct statistics {
        unsigned int modulus_bit_size;  // bit size of modulus and base
        unsigned int exponent_bit_size; // bit size of exponent
        int64_t      min_time_ns;
        int64_t      max_time_ns;
        int64_t      avg_time_ns;
    }; 
 
    std::vector<statistics> stats;
 
    auto ceil_log2 = [](uint32_t n) -> uint32_t {
        if (n <= 1) {
            return 0;
        }
        return 32 - __builtin_clz(n - 1);
    };
 
    BOOST_CHECK(ceil_log2(0) == 0);
    BOOST_CHECK(ceil_log2(1) == 0);
    BOOST_CHECK(ceil_log2(2) == 1);
    BOOST_CHECK(ceil_log2(3) == 2);
    BOOST_CHECK(ceil_log2(4) == 2);
    BOOST_CHECK(ceil_log2(5) == 3);
    BOOST_CHECK(ceil_log2(15) == 4);
    BOOST_CHECK(ceil_log2(16) == 4);
    BOOST_CHECK(ceil_log2(17) == 5);
 
    for (unsigned int n = start_num_bytes; n <= end_num_bytes; n *= 2) {
        unsigned int bit_calc = 8 * ceil_log2(n);
        for (unsigned int exponent_num_bytes = 1; 
             exponent_num_bytes <= 2*n && bit_calc <= bit_calc_limit; 
             exponent_num_bytes *= 2, bit_calc += 5) 
        {
            int64_t min_duration_ns = std::numeric_limits<int64_t>::max();
            int64_t max_duration_ns = 0;
            int64_t total_duration_ns = 0;
 
            for (unsigned int trial = 0; trial < num_trials; ++trial) {
                auto base     = generate_random_bytes(r, n);
                auto exponent = generate_random_bytes(r, exponent_num_bytes);
                auto modulus  = generate_random_bytes(r, n);
 
                auto start_time = std::chrono::steady_clock::now();
 
                auto res = fc::modexp(base, exponent, modulus);
 
                auto end_time = std::chrono::steady_clock::now();
 
                int64_t duration_ns = std::chrono::duration_cast<std::chrono::nanoseconds>(end_time - start_time).count();
 
                //ilog("(${base})^(${exp}) % ${mod} = ${result} [took ${duration} ns]", 
                //     ("base", base)("exp", exponent)("mod", modulus)("result", std::get<bytes>(res))("duration", duration_ns)
                //    );
 
                min_duration_ns = std::min(min_duration_ns, duration_ns);
                max_duration_ns = std::max(max_duration_ns, duration_ns);
                total_duration_ns += duration_ns;
            }
 
            stats.push_back(statistics{
                .modulus_bit_size  = n * 8,
                .exponent_bit_size = exponent_num_bytes * 8, 
                .min_time_ns       = min_duration_ns,
                .max_time_ns       = max_duration_ns,
                .avg_time_ns       = (total_duration_ns / num_trials),
            });
 
            const auto& stat = stats.back();
 
            ilog("Completed random runs of mod_exp with ${bit_width}-bit width base and modulus values and "
                 "${exp_bit_width}-bit width exponent values. "
                 "Min time: ${min} ns; Average time: ${avg} ns; Max time: ${max} ns.",
                ("bit_width", stat.modulus_bit_size)("exp_bit_width", stat.exponent_bit_size)
                ("min", stat.min_time_ns)("avg", stat.avg_time_ns)("max", stat.max_time_ns)
                );
 
        }
    }
 
    std::string stats_output = "Table (in csv format) summarizing statistics from runs:\n";
    stats_output += "Modulus/Base Bit Size,Exponent Bit Size,Average Time (ns)\n";
    for (const auto& stat : stats) {
        stats_output += std::to_string(stat.modulus_bit_size);
        stats_output += ',';
        stats_output += std::to_string(stat.exponent_bit_size);
        stats_output += ',';
        stats_output += std::to_string(stat.avg_time_ns);
        stats_output += '\n';
    }
 
    ilog(stats_output);
 
    // Running the above benchmark (using commented values for num_trials and bit_calc_limit) with a release build on 
    // an AMD 3.4 GHz CPU provides average durations for executing mod_exp for varying bit sizes for the values 
    // (but with base and modulus bit sizes kept equal to one another).
 
    // Holding the base/modulus bit size constant and increasing the exponent bit size shows a linear relationship with increasing bit
    // size on the average time to execute the modular exponentiation. The slope of the best fit line to the empirical data appears
    // to scale super-linearly with base/modulus size. A quadratic (degree 2) fit works okay, but it appears that a better fit is to
    // model the slope of the linear relationship between average time and exponent bit size as a the base/modulus bit size taken to
    // the 1.6 power and then scaled by some constant.
 
    // Holding the exponent bit size constant and increasing the base/modulus bit size shows a super-linear relationship with
    // increasing bit size on the average time to execute the modular exponentiation. A quadratic relationship works pretty well
    // but perhaps a fractional exponent between 1 and 2 (e.g. 1.6) would work well as well.
    
    // What is particularly revealing is plotting the average time with respect to some combination of the bit sizes of base/modulus and
    // exponent. If the independent variable is the product of the exponent bit size and the base/modulus bit size, the correlation is
    // not great. Even if the independent variable is the product of the exponent bit size and the base/modulus bit size taken to some power,
    // the correlation is still not great.
    // It seems that trying to capture all the data using a model like that breaks down when the exponent bit size is greater than the
    // base/modulus bit size.
    // If we filter out all the data points where the exponent bit size is greater than the base/modulus bit size, and then choose as
    // then independent variable the product of the exponent bit size and the base/modulus bit size taken to some power, then we get
    // a pretty good linear correlation when a power of 1.6 is chosen.
 
    // TODO: See if theoretical analysis of the modular exponentiation algorithm also justifies these scaling properties.
 
    // Example results for average time:
    // | Modulus/Base Bit Size | Exponent Bit Size | Average Time (ns) |
    // | --------------------- | ----------------- | ----------------- |
    // | 2048                  | 32                |             33826 |
    // | 2048                  | 256               |            250067 |
    // | 2048                  | 2048              |           1891095 |
    // | 4096                  | 32                |            129181 |
    // | 4096                  | 256               |            954024 |
    // | 4096                  | 2048              |           7205115 |
    // | 8192                  | 32                |            347938 |
    // | 8192                  | 256               |           2503652 |
    // | 8192                  | 2048              |          19199775 |
 
    // The empirical results show that the average time stays well below 5 ms if the exponent bit size does not exceed the
    // modulus/base bit size and the product of the exponent bit size and the 
    // (modulus/base bit size)^1.6 does not exceed 550,000,000.
    // Another way of satisfying that constraint is to require that the 5*ceil(log2(exponent bit size)) + 8*ceil(log2(modulus bit size)) 
    // be less than or equal to 5*floor(log2(500000000)) = 145.
    // Or equivalently, assuming the bit sizes are multiples of 8:
    // 5*ceil(log2(exponent bit size/8)) + 8*ceil(log2(modulus bit size/8)) <= 106.
 
    // Take, as an example, a 8192-bit modulus/base and a 128-bit exponent (which on average took 1.29 ms).
    // 5*ceil(log2(128)) + 8*ceil(log2(8192)) = 5*7 + 8*13 = 139 which is less than the limit of 145.
    // 
    // Or, as an other example, a 2048-bit modulus/base and a 2048-bit exponent (which on average took 1.89 ms).
    // 5*ceil(log2(2048)) + 8*ceil(log2(2048)) = 5*11 + 8*11 = 143 which is less than the limit of 145.
    //
    // On the other hand, consider a 4096-bit modulus/base and a 1024-bit exponent (which on average took 3.69 ms).
    // 5*ceil(log2(1024)) + 8*ceil(log2(4096)) = 5*10 + 8*12 = 146 which is greater than the limit of 145.
 
} FC_LOG_AND_RETHROW();

Here is the call graph for this function:

FC_LOG_AND_RETHROW()

FC_LOG_AND_RETHROW

(

)