bn::Fp12T< T > Struct Template Reference

#include <bn.h>

Inheritance diagram for bn::Fp12T< T >:

Collaboration diagram for bn::Fp12T< T >:

Classes
struct	Dbl

Public Types
typedef T	Fp6
typedef Fp6::Fp2	Fp2
typedef Fp6::Fp	Fp
typedef ParamT< Fp2 >	Param
typedef Fp2::Dbl	Fp2Dbl
typedef Fp6::Dbl	Fp6Dbl

Public Member Functions
	Fp12T ()
	Fp12T (int x)
	Fp12T (const Fp6 &a, const Fp6 &b)
	Fp12T (const Fp &a0, const Fp &a1, const Fp &a2, const Fp &a3, const Fp &a4, const Fp &a5, const Fp &a6, const Fp &a7, const Fp &a8, const Fp &a9, const Fp &a10, const Fp &a11)
	Fp12T (const Fp2 &a0, const Fp2 &a1, const Fp2 &a2, const Fp2 &a3, const Fp2 &a4, const Fp2 &a5)
void	clear ()
Fp *	get ()
const Fp *	get () const
Fp2 *	getFp2 ()
const Fp2 *	getFp2 () const
void	set (const Fp2 &v0, const Fp2 &v1, const Fp2 &v2, const Fp2 &v3, const Fp2 &v4, const Fp2 &v5)
bool	isZero () const
bool	operator== (const Fp12T &rhs) const
bool	operator!= (const Fp12T &rhs) const
void	Fp2_2z_add_3x (Fp2 &z, const Fp2 &x)
void	sqru ()
void	sqru (Fp12T &zz) const
void	inverse ()
void	Frobenius (Fp12T &z) const
void	Frobenius2 (Fp12T &z) const
void	Frobenius3 (Fp12T &z) const
void	mapToCyclo (Fp12T &z)
void	final_exp ()
Public Member Functions inherited from mie::local::addsubmul< Fp12T< T > >
MIE_FORCE_INLINE T &	operator+= (const N &rhs)
MIE_FORCE_INLINE T &	operator-= (const T &rhs)
MIE_FORCE_INLINE T &	operator*= (const T &rhs)

Static Public Member Functions
static void	add (Fp12T &z, const Fp12T &x, const Fp12T &y)
static void	sub (Fp12T &z, const Fp12T &x, const Fp12T &y)
static void	neg (Fp12T &z, const Fp12T &x)
static void	mulC (Fp12T &z, const Fp12T &x, const Fp12T &y)
static void	squareC (Fp12T &z)
static void	sq_Fp4UseDbl (Fp2 &z0, Fp2 &z1, const Fp2 &x0, const Fp2 &x1)

Public Attributes
Fp6	a_
Fp6	b_

Static Public Attributes
static void(*	mul )(Fp12T &z, const Fp12T &x, const Fp12T &y)
static void(*	square )(Fp12T &z)

Friends
std::ostream &	operator<< (std::ostream &os, const Fp12T &x)
std::istream &	operator>> (std::istream &is, Fp12T &x)

Detailed Description

template<class T>
struct bn::Fp12T< T >

Definition at line 1363 of file bn.h.

Member Typedef Documentation

Fp

template<class T >

Fp6::Fp bn::Fp12T< T >::Fp

Definition at line 1366 of file bn.h.

Fp2

template<class T >

Fp6::Fp2 bn::Fp12T< T >::Fp2

Definition at line 1365 of file bn.h.

Fp2Dbl

template<class T >

Fp2::Dbl bn::Fp12T< T >::Fp2Dbl

Definition at line 1368 of file bn.h.

Fp6

template<class T >

T bn::Fp12T< T >::Fp6

Definition at line 1364 of file bn.h.

Fp6Dbl

template<class T >

Fp6::Dbl bn::Fp12T< T >::Fp6Dbl

Definition at line 1369 of file bn.h.

Param

template<class T >

ParamT<Fp2> bn::Fp12T< T >::Param

Definition at line 1367 of file bn.h.

Constructor & Destructor Documentation

Fp12T() [1/5]

template<class T >

bn::Fp12T< T >::Fp12T ( )

inline

Definition at line 1372 of file bn.h.

{ }

Fp12T() [2/5]

template<class T >

bn::Fp12T< T >::Fp12T ( int x )

inline

Definition at line 1373 of file bn.h.

        : a_(x)
        , b_(0)
    {
    }

Fp12T() [3/5]

template<class T >

bn::Fp12T< T >::Fp12T ( const Fp6 & a, const Fp6 & b )

inline

Definition at line 1378 of file bn.h.

        : a_(a)
        , b_(b)
    {
    }

Fp12T() [4/5]

template<class T >

bn::Fp12T< T >::Fp12T ( const Fp & a0, const Fp & a1, const Fp & a2, const Fp & a3, const Fp & a4, const Fp & a5, const Fp & a6, const Fp & a7, const Fp & a8, const Fp & a9, const Fp & a10, const Fp & a11 )

inline

Definition at line 1383 of file bn.h.

        : a_(a0, a1, a2, a3, a4, a5)
        , b_(a6, a7, a8, a9, a10, a11)
    {
    }

Fp12T() [5/5]

template<class T >

bn::Fp12T< T >::Fp12T ( const Fp2 & a0, const Fp2 & a1, const Fp2 & a2, const Fp2 & a3, const Fp2 & a4, const Fp2 & a5 )

inline

Definition at line 1390 of file bn.h.

        : a_(a0, a1, a2)
        , b_(a3, a4, a5)
    {
    }

Member Function Documentation

add()

template<class T >

static void bn::Fp12T< T >::add ( Fp12T< T > & z, const Fp12T< T > & x, const Fp12T< T > & y )

inlinestatic

Definition at line 1432 of file bn.h.

    {
        Fp6::add(z.a_, x.a_, y.a_);
        Fp6::add(z.b_, x.b_, y.b_);
    }

Here is the caller graph for this function:

clear()

template<class T >

void bn::Fp12T< T >::clear ( )

inline

Definition at line 1396 of file bn.h.

    {
        a_.clear();
        b_.clear();
    }

Here is the caller graph for this function:

final_exp()

template<class T >

void bn::Fp12T< T >::final_exp ( )

inline

Definition at line 1776 of file bn.h.

    {
        Fp12T f, f2z, f6z, f6z2, f12z3;
        Fp12T a, b;
        Fp12T& z = *this;
        mapToCyclo(f);
 
#ifdef BN_SUPPORT_SNARK
        Fp12T::pow_neg_t(f2z, f);
        f2z.sqru(); // f2z = f^(-2*z)
        f2z.sqru(f6z);
        f6z *= f2z; // f6z = f^(-6*z)
        Fp12T::pow_neg_t(f6z2, f6z);
        // A variable a is unnecessary only here.
        f6z2.sqru(a);
        // Compress::fixed_power(f12z3, a); // f12z3 = f^(-12*z^3)
        Fp12T::pow_neg_t(f12z3, a);
        // It will compute inversion of f2z, thus, conjugation free.
        Fp6::neg(f6z.b_, f6z.b_); // f6z = f^(6z)
        Fp6::neg(f12z3.b_, f12z3.b_); // f12z3 = f^(12*z^3)
        // Computes a and b.
        Fp12T::mul(a, f12z3, f6z2); // a = f^(12*z^3 + 6z^2)
        a *= f6z; // a = f^(12*z^3 + 6z^2 + 6z)
        Fp12T::mul(b, a, f2z); // b = f^(12*z^3 + 6z^2 + 4z)w
        // @note f2z, f6z, and f12z are unnecessary from here.
        // Last part.
        Fp12T::mul(z, a, f6z2); // z = f^(12*z^3 + 12z^2 + 6z)
        z *= f; // z = f^(12*z^3 + 12z^2 + 6z + 1)
        b.Frobenius(f2z); // f2z = f^(q(12*z^3 + 6z^2 + 4z))
        z *= f2z; // z = f^(q(12*z^3 + 6z^2 + 4z) + (12*z^3 + 12z^2 + 6z + 1))
        a.Frobenius2(f2z); // f2z = f^(q^2(12*z^3 + 6z^2 + 6z))
        z *= f2z; // z = f^(q^2(12*z^3 + 6z^2 + 6z) + q(12*z^3 + 6z^2 + 4z) + (12*z^3 + 12z^2 + 6z + 1))
        Fp6::neg(f.b_, f.b_); // f = -f
        b *= f; // b = f^(12*z^3 + 6z^2 + 4z - 1)
        b.Frobenius3(f2z); // f2z = f^(q^3(12*z^3 + 6z^2 + 4z - 1))
        z *= f2z;
        // z = f^(q^3(12*z^3 + 6z^2 + 4z - 1) +
        // q^2(12*z^3 + 6z^2 + 6z) +
        // q(12*z^3 + 6z^2 + 4z) +
        // (12*z^3 + 12z^2 + 6z + 1))
        // see page 6 in the "Faster hashing to G2" paper
#else
        // Hard part starts from here.
        // Computes addition chain.
        typedef CompressT<Fp2> Compress;
        Compress::fixed_power(f2z, f);
        f2z.sqru();
        f2z.sqru(f6z);
        f6z *= f2z;
        Compress::fixed_power(f6z2, f6z);
        // A variable a is unnecessary only here.
        f6z2.sqru(a);
        Compress::fixed_power(f12z3, a);
        // It will compute inversion of f2z, thus, conjugation free.
        Fp6::neg(f6z.b_, f6z.b_);
        Fp6::neg(f12z3.b_, f12z3.b_);
        // Computes a and b.
        Fp12T::mul(a, f12z3, f6z2);
        a *= f6z;
        Fp12T::mul(b, a, f2z);
        // @note f2z, f6z, and f12z are unnecessary from here.
        // Last part.
        Fp12T::mul(z, a, f6z2);
        z *= f;
        b.Frobenius(f2z);
        z *= f2z;
        a.Frobenius2(f2z);
        z *= f2z;
        Fp6::neg(f.b_, f.b_);
        b *= f;
        b.Frobenius3(f2z);
        z *= f2z;
#endif
    }

Here is the call graph for this function:

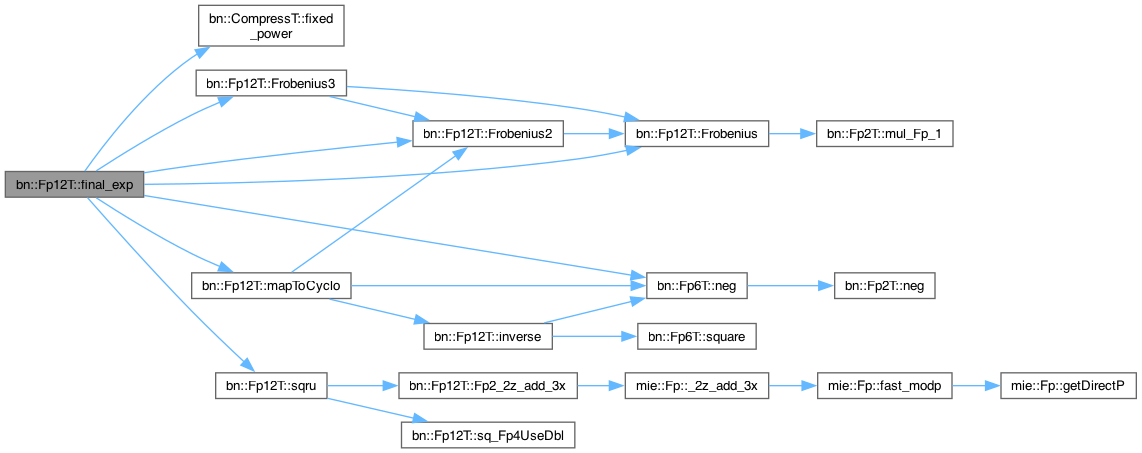
Here is the caller graph for this function:

Fp2_2z_add_3x()

template<class T >

void bn::Fp12T< T >::Fp2_2z_add_3x ( Fp2 & z, const Fp2 & x )

inline

Definition at line 1556 of file bn.h.

    {
        Fp::_2z_add_3x(z.a_, x.a_);
        Fp::_2z_add_3x(z.b_, x.b_);
    }

Here is the call graph for this function:

Here is the caller graph for this function:

Frobenius()

template<class T >

void bn::Fp12T< T >::Frobenius ( Fp12T< T > & z ) const

inline

Definition at line 1640 of file bn.h.

    {
        /* this assumes (q-1)/6 is odd */
        if (&z != this) {
            z.a_.a_.a_ = a_.a_.a_;
            z.a_.b_.a_ = a_.b_.a_;
            z.a_.c_.a_ = a_.c_.a_;
            z.b_.a_.a_ = b_.a_.a_;
            z.b_.b_.a_ = b_.b_.a_;
            z.b_.c_.a_ = b_.c_.a_;
        }
        Fp::neg(z.a_.a_.b_, a_.a_.b_);
        Fp::neg(z.a_.b_.b_, a_.b_.b_);
        Fp::neg(z.a_.c_.b_, a_.c_.b_);
        Fp::neg(z.b_.a_.b_, b_.a_.b_);
        Fp::neg(z.b_.b_.b_, b_.b_.b_);
        Fp::neg(z.b_.c_.b_, b_.c_.b_);
#ifdef BN_SUPPORT_SNARK
        z.a_.b_ *= Param::gammar[1];
        z.a_.c_ *= Param::gammar[3];
#else
        assert(Param::gammar[1].a_ == 0);
        assert(Param::gammar[3].b_ == 0);
        Fp2::mul_Fp_1(z.a_.b_, Param::gammar[1].b_);
        Fp2::mul_Fp_0(z.a_.c_, z.a_.c_, Param::gammar[3].a_);
#endif
        z.b_.a_ *= Param::gammar[0];
        z.b_.b_ *= Param::gammar[2];
        z.b_.c_ *= Param::gammar[4];
    }

Here is the call graph for this function:

Here is the caller graph for this function:

Frobenius2()

template<class T >

void bn::Fp12T< T >::Frobenius2 ( Fp12T< T > & z ) const

inline

Definition at line 1678 of file bn.h.

    {
#if 0
        Frobenius(z);
        z.Frobenius(z);
#else
        if (&z != this) {
            z.a_.a_ = a_.a_;
        }
        z.a_.a_ = a_.a_;
        Fp2::mul_Fp_0(z.a_.b_, a_.b_, Param::gammar2[1].a_);
        Fp2::mul_Fp_0(z.a_.c_, a_.c_, Param::gammar2[3].a_);
        Fp2::mul_Fp_0(z.b_.a_, b_.a_, Param::gammar2[0].a_);
        Fp2::mul_Fp_0(z.b_.b_, b_.b_, Param::gammar2[2].a_);
        Fp2::mul_Fp_0(z.b_.c_, b_.c_, Param::gammar2[4].a_);
#endif
    }

Here is the call graph for this function:

Here is the caller graph for this function:

Frobenius3()

template<class T >

void bn::Fp12T< T >::Frobenius3 ( Fp12T< T > & z ) const

inline

Definition at line 1696 of file bn.h.

    {
#if 0
        Frobenius2(z);
        z.Frobenius(z);
#else
        z.a_.a_.a_ = a_.a_.a_;
        z.a_.b_.a_ = a_.b_.a_;
        z.a_.c_.a_ = a_.c_.a_;
        z.b_.a_.a_ = b_.a_.a_;
        z.b_.b_.a_ = b_.b_.a_;
        z.b_.c_.a_ = b_.c_.a_;
        Fp::neg(z.a_.a_.b_, a_.a_.b_);
        Fp::neg(z.a_.b_.b_, a_.b_.b_);
        Fp::neg(z.a_.c_.b_, a_.c_.b_);
        Fp::neg(z.b_.a_.b_, b_.a_.b_);
        Fp::neg(z.b_.b_.b_, b_.b_.b_);
        Fp::neg(z.b_.c_.b_, b_.c_.b_);
 
#ifdef BN_SUPPORT_SNARK
        z.a_.b_ *= Param::gammar3[1];
        z.a_.c_ *= Param::gammar3[3];
#else
        z.a_.b_.mul_x();
        Fp2::mul_Fp_0(z.a_.c_, z.a_.c_, Param::gammar3[3].a_);
#endif
        z.b_.a_ *= Param::gammar3[0];
        z.b_.b_ *= Param::gammar3[2];
        z.b_.c_ *= Param::gammar3[4];
#endif
    }

Here is the call graph for this function:

Here is the caller graph for this function:

get() [1/2]

template<class T >

Fp * bn::Fp12T< T >::get ( )

inline

Definition at line 1402 of file bn.h.

{ return a_.get(); }

get() [2/2]

template<class T >

const Fp * bn::Fp12T< T >::get ( ) const

inline

Definition at line 1403 of file bn.h.

{ return a_.get(); }

getFp2() [1/2]

template<class T >

Fp2 * bn::Fp12T< T >::getFp2 ( )

inline

Definition at line 1404 of file bn.h.

{ return a_.getFp2(); }

Here is the caller graph for this function:

getFp2() [2/2]

template<class T >

const Fp2 * bn::Fp12T< T >::getFp2 ( ) const

inline

Definition at line 1405 of file bn.h.

{ return a_.getFp2(); }

inverse()

template<class T >

void bn::Fp12T< T >::inverse ( )

inline

Definition at line 1620 of file bn.h.

    {
        Fp6 tmp0;
        Fp6 tmp1;
        Fp2 tmp2;
        Fp6::square(tmp0, a_);
        Fp6::square(tmp1, b_);
        Fp2::mul_xi(tmp2, tmp1.c_);
        tmp0.a_ -= tmp2;
        tmp0.b_ -= tmp1.a_;
        tmp0.c_ -= tmp1.b_;
        tmp0.inverse();
        Fp6::mul(a_, a_, tmp0);
        Fp6::mul(b_, b_, tmp0);
        Fp6::neg(b_, b_);
    }

Here is the call graph for this function:

Here is the caller graph for this function:

isZero()

template<class T >

bool bn::Fp12T< T >::isZero ( ) const

inline

Definition at line 1412 of file bn.h.

    {
        return a_.isZero() && b_.isZero();
    }

mapToCyclo()

template<class T >

void bn::Fp12T< T >::mapToCyclo ( Fp12T< T > & z )

inline

Definition at line 1731 of file bn.h.

    {
        // (a + b*i) -> ((a - b*i) * (a + b*i)^(-1))^(q^2+1)
        //
        // See Beuchat page 9: raising to 6-th power is the same as
        // conjugation, so this entire function computes
        // z^((p^6-1) * (p^2+1))
        z.a_ = a_;
        Fp6::neg(z.b_, b_);
        inverse();
        z *= *this;
        z.Frobenius2(*this);
        z *= *this;
    }

Here is the call graph for this function:

Here is the caller graph for this function:

mulC()

template<class T >

static void bn::Fp12T< T >::mulC ( Fp12T< T > & z, const Fp12T< T > & x, const Fp12T< T > & y )

inlinestatic

Definition at line 1450 of file bn.h.

    {
        Dbl zd;
        Fp6 t0, t1;
        Fp6Dbl T0, T1, T2;
        // # 1
        Fp6Dbl::mul(T0, x.a_, y.a_);
        Fp6Dbl::mul(T1, x.b_, y.b_);
        Fp6::add(t0, x.a_, x.b_);
        Fp6::add(t1, y.a_, y.b_);
        // # 2
        Fp6Dbl::mul(zd.a_, t0, t1);
        // # 3
        Fp6Dbl::add(T2, T0, T1);
        // # 4
        Fp6Dbl::sub(zd.b_, zd.a_, T2);
        // #6, 7, 8
        mul_gamma_add<Fp6Dbl, Fp2Dbl>(zd.a_, T1, T0);
        Dbl::mod(z, zd);
    }

Here is the call graph for this function:

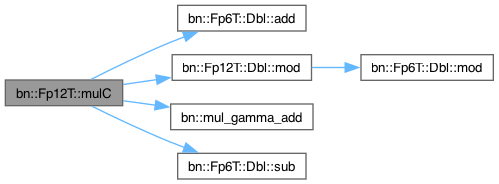
neg()

template<class T >

static void bn::Fp12T< T >::neg ( Fp12T< T > & z, const Fp12T< T > & x )

inlinestatic

Definition at line 1442 of file bn.h.

    {
        Fp6::neg(z.a_, x.a_);
        Fp6::neg(z.b_, x.b_);
    }

Here is the call graph for this function:

operator!=()

template<class T >

bool bn::Fp12T< T >::operator!= ( const Fp12T< T > & rhs ) const

inline

Definition at line 1420 of file bn.h.

{ return !operator==(rhs); }

Here is the call graph for this function:

operator==()

template<class T >

bool bn::Fp12T< T >::operator== ( const Fp12T< T > & rhs ) const

inline

Definition at line 1416 of file bn.h.

    {
        return a_ == rhs.a_ && b_ == rhs.b_;
    }

Here is the caller graph for this function:

set()

template<class T >

void bn::Fp12T< T >::set ( const Fp2 & v0, const Fp2 & v1, const Fp2 & v2, const Fp2 & v3, const Fp2 & v4, const Fp2 & v5 )

inline

Definition at line 1406 of file bn.h.

    {
        a_.set(v0, v1, v2);
        b_.set(v3, v4, v5);
    }

sq_Fp4UseDbl()

template<class T >

static void bn::Fp12T< T >::sq_Fp4UseDbl ( Fp2 & z0, Fp2 & z1, const Fp2 & x0, const Fp2 & x1 )

inlinestatic

Definition at line 1509 of file bn.h.

    {
        Fp2Dbl T0, T1, T2;
        Fp2Dbl::square(T0, x0);
        Fp2Dbl::square(T1, x1);
        Fp2Dbl::mul_xi(T2, T1);
        T2 += T0;
        Fp2::add(z1, x0, x1);
        Fp2Dbl::mod(z0, T2);
        // overwrite z[0] (position 0).
        Fp2Dbl::square(T2, z1);
        T2 -= T0;
        T2 -= T1;
        Fp2Dbl::mod(z1, T2);
    }

Here is the caller graph for this function:

sqru() [1/2]

template<class T >

void bn::Fp12T< T >::sqru ( )

inline

Definition at line 1561 of file bn.h.

    {
        Fp2& z0(a_.a_);
        Fp2& z4(a_.b_);
        Fp2& z3(a_.c_);
        Fp2& z2(b_.a_);
        Fp2& z1(b_.b_);
        Fp2& z5(b_.c_);
        Fp2 t0, t1;
        sq_Fp4UseDbl(t0, t1, z0, z1); // a^2 = t0 + t1*y
        // For A
        Fp2::sub(z0, t0, z0);
        z0 += z0;
        z0 += t0;
#if 0
        Fp2_2z_add_3x(z1, t1);
#else
        Fp2::add(z1, t1, z1);
        z1 += z1;
        z1 += t1;
#endif
        // t0 and t1 are unnecessary from here.
        Fp2 t2, t3;
        sq_Fp4UseDbl(t0, t1, z2, z3); // b^2 = t0 + t1*y
        sq_Fp4UseDbl(t2, t3, z4, z5); // c^2 = t2 + t3*y
        // For C
        Fp2::sub(z4, t0, z4);
        z4 += z4;
        z4 += t0;
#if 0
        Fp2_2z_add_3x(z5, t1);
#else
        Fp2::add(z5, t1, z5);
        z5 += z5;
        z5 += t1;
#endif
        // For B
        Fp2::mul_xi(t0, t3);
#if 0
        Fp2_2z_add_3x(z2, t0);
#else
        Fp2::add(z2, t0, z2);
        z2 += z2;
        z2 += t0;
#endif
        Fp2::sub(z3, t2, z3);
        z3 += z3;
        z3 += t2;
    }

Here is the call graph for this function:

Here is the caller graph for this function:

sqru() [2/2]

template<class T >

void bn::Fp12T< T >::sqru ( Fp12T< T > & zz ) const

inline

Definition at line 1614 of file bn.h.

    {
        zz = *this;
        zz.sqru();
    }

Here is the call graph for this function:

squareC()

template<class T >

static void bn::Fp12T< T >::squareC ( Fp12T< T > & z )

inlinestatic

Definition at line 1476 of file bn.h.

    {
        Fp6 t0, t1;
        // # 1, 2
        Fp6::add(t0, z.a_, z.b_);
        // b_.mul_gamma(t1); t1 += a_; # 3
        mul_gamma_add<Fp6, Fp2>(t1, z.b_, z.a_);
        // # 4
        z.b_ *= z.a_;
        Fp6::mul(z.a_, t0, t1);
        // # 5, 6, 7 @note It's typo.
        mul_gamma_add<Fp6, Fp2>(t1, z.b_, z.b_);
        // # 8
        z.a_ -= t1;
        z.b_ += z.b_;
    }

Here is the call graph for this function:

sub()

template<class T >

static void bn::Fp12T< T >::sub ( Fp12T< T > & z, const Fp12T< T > & x, const Fp12T< T > & y )

inlinestatic

Definition at line 1437 of file bn.h.

    {
        Fp6::sub(z.a_, x.a_, y.a_);
        Fp6::sub(z.b_, x.b_, y.b_);
    }

Here is the caller graph for this function:

Friends And Related Symbol Documentation

operator<<

template<class T >

std::ostream & operator<< ( std::ostream & os, const Fp12T< T > & x )

friend

Definition at line 1421 of file bn.h.

    {
        return os << "[" << x.a_ << ",\n " << x.b_ << "]";
    }

operator>>

template<class T >

std::istream & operator>> ( std::istream & is, Fp12T< T > & x )

friend

Definition at line 1425 of file bn.h.

    {
        char c1, c2, c3;
        is >> c1 >> x.a_ >> c2 >> x.b_ >> c3;
        if (c1 == '[' && c2 == ',' && c3 == ']') return is;
        throw std::ios_base::failure("bad Fp12");
    }

Member Data Documentation

a_

template<class T >

Fp6 bn::Fp12T< T >::a_

Definition at line 1371 of file bn.h.

b_

template<class T >

Fp6 bn::Fp12T< T >::b_

Definition at line 1371 of file bn.h.

mul

template<class T >

void(* bn::Fp12T< T >::mul) (Fp12T &z, const Fp12T &x, const Fp12T &y)

static

Definition at line 1449 of file bn.h.

square

template<class T >

void(* bn::Fp12T< T >::square) (Fp12T &z)

static

Definition at line 1475 of file bn.h.

---

The documentation for this struct was generated from the following file:

• libraries/fc/libraries/ff/depends/ate-pairing/include/bn.h