Wire Sysio Wire Sysion 1.0.0
Loading...
Searching...
No Matches
Classes | Macros | Typedefs | Enumerations | Functions | Variables
dtoa.c File Reference
#include "stdlib.h"
#include "string.h"
#include "errno.h"
#include "float.h"
#include "math.h"
Include dependency graph for dtoa.c:
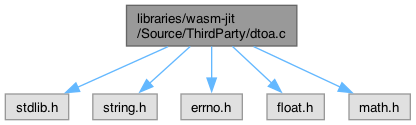
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes

union  U
 
struct  BCinfo
 
struct  Bigint
 

Macros

#define Long   long
 
#define MALLOC   malloc
 
#define PRIVATE_MEM   2304
 
#define PRIVATE_mem   ((PRIVATE_MEM+sizeof(double)-1)/sizeof(double))
 
#define NO_STRTOD_BIGCOMP
 
#define CONST   const
 
#define word0(x)
 
#define word1(x)
 
#define dval(x)
 
#define STRTOD_DIGLIM   40
 
#define strtod_diglim   STRTOD_DIGLIM
 
#define Storeinc(a, b, c)
 
#define Sudden_Underflow
 
#define Flt_Rounds   1
 
#define Exp_shift   23
 
#define Exp_shift1   7
 
#define Exp_msk1   0x80
 
#define Exp_msk11   0x800000
 
#define Exp_mask   0x7f80
 
#define P   56
 
#define Nbits   56
 
#define Bias   129
 
#define Emax   126
 
#define Emin   (-129)
 
#define Exp_1   0x40800000
 
#define Exp_11   0x4080
 
#define Ebits   8
 
#define Frac_mask   0x7fffff
 
#define Frac_mask1   0xffff007f
 
#define Ten_pmax   24
 
#define Bletch   2
 
#define Bndry_mask   0xffff007f
 
#define Bndry_mask1   0xffff007f
 
#define LSB   0x10000
 
#define Sign_bit   0x8000
 
#define Log2P   1
 
#define Tiny0   0x80
 
#define Tiny1   0
 
#define Quick_max   15
 
#define Int_max   15
 
#define ROUND_BIASED
 
#define rounded_product(a, b)
 
#define rounded_quotient(a, b)
 
#define Big0   (Frac_mask1 | Exp_msk1*(DBL_MAX_EXP+Bias-1))
 
#define Big1   0xffffffff
 
#define Pack_32
 
#define FFFFFFFF   0xffffffffUL
 
#define Llong   long long
 
#define ULLong   unsigned Llong
 
#define ACQUIRE_DTOA_LOCK(n)
 
#define FREE_DTOA_LOCK(n)
 
#define Kmax   7
 
#define Bcopy(x, y)
 
#define d0   word0(&d)
 
#define d1   word1(&d)
 
#define d0   word0(d)
 
#define d1   word1(d)
 
#define n_bigtens   2
 
#define Need_Hexdig
 
#define ULbits   32
 
#define kshift   5
 
#define kmask   31
 

Typedefs

typedef unsigned Long ULong
 
typedef struct BCinfo BCinfo
 
typedef struct Bigint Bigint
 

Enumerations

enum  { Round_zero = 0 , Round_near = 1 , Round_up = 2 , Round_down = 3 }
 

Functions

void gethex (CONST char **sp, U *rvp, int rounding, int sign)
 
double strtod (const char *s00, char **se)
 
void freedtoa (char *s)
 
char * dtoa (double dd, int mode, int ndigits, int *decpt, int *sign, char **rve)
 

Variables

Exactly one of IEEE_8087
 
Exactly one of IEEE_MC68k
 
Exactly one of VAX
 

Macro Definition Documentation

◆ ACQUIRE_DTOA_LOCK

#define ACQUIRE_DTOA_LOCK ( n)
Value:
/*nothing*/

Definition at line 520 of file dtoa.c.

◆ Bcopy

#define Bcopy ( x,
y )
Value:
memcpy((char *)&x->sign, (char *)&y->sign, \
y->wds*sizeof(Long) + 2*sizeof(int))
Long
#define Long
Definition dtoa.c:190
memcpy
memcpy((char *) pInfo->slotDescription, s, l)

Definition at line 608 of file dtoa.c.

608#define Bcopy(x,y) memcpy((char *)&x->sign, (char *)&y->sign, \
609y->wds*sizeof(Long) + 2*sizeof(int))

◆ Bias

#define Bias   129

Definition at line 439 of file dtoa.c.

◆ Big0

#define Big0   (Frac_mask1 | Exp_msk1*(DBL_MAX_EXP+Bias-1))

Definition at line 483 of file dtoa.c.

◆ Big1

#define Big1   0xffffffff

Definition at line 484 of file dtoa.c.

◆ Bletch

#define Bletch   2

Definition at line 448 of file dtoa.c.

◆ Bndry_mask

#define Bndry_mask   0xffff007f

Definition at line 449 of file dtoa.c.

◆ Bndry_mask1

#define Bndry_mask1   0xffff007f

Definition at line 450 of file dtoa.c.

◆ CONST

#define CONST   const

Definition at line 298 of file dtoa.c.

◆ d0 [1/2]

#define d0   word0(&d)

◆ d0 [2/2]

#define d0   word0(d)

◆ d1 [1/2]

#define d1   word1(&d)

◆ d1 [2/2]

#define d1   word1(d)

◆ dval

#define dval ( x)
Value:
(x)->d

Definition at line 315 of file dtoa.c.

◆ Ebits

#define Ebits   8

Definition at line 444 of file dtoa.c.

◆ Emax

#define Emax   126

Definition at line 440 of file dtoa.c.

◆ Emin

#define Emin   (-129)

Definition at line 441 of file dtoa.c.

◆ Exp_1

#define Exp_1   0x40800000

Definition at line 442 of file dtoa.c.

◆ Exp_11

#define Exp_11   0x4080

Definition at line 443 of file dtoa.c.

◆ Exp_mask

#define Exp_mask   0x7f80

Definition at line 436 of file dtoa.c.

◆ Exp_msk1

#define Exp_msk1   0x80

Definition at line 434 of file dtoa.c.

◆ Exp_msk11

#define Exp_msk11   0x800000

Definition at line 435 of file dtoa.c.

◆ Exp_shift

#define Exp_shift   23

Definition at line 432 of file dtoa.c.

◆ Exp_shift1

#define Exp_shift1   7

Definition at line 433 of file dtoa.c.

◆ FFFFFFFF

#define FFFFFFFF   0xffffffffUL

Definition at line 497 of file dtoa.c.

◆ Flt_Rounds

#define Flt_Rounds   1

Definition at line 431 of file dtoa.c.

◆ Frac_mask

#define Frac_mask   0x7fffff

Definition at line 445 of file dtoa.c.

◆ Frac_mask1

#define Frac_mask1   0xffff007f

Definition at line 446 of file dtoa.c.

◆ FREE_DTOA_LOCK

#define FREE_DTOA_LOCK ( n)
Value:
/*nothing*/

Definition at line 521 of file dtoa.c.

◆ Int_max

#define Int_max   15

Definition at line 457 of file dtoa.c.

◆ kmask

#define kmask   31

Definition at line 1644 of file dtoa.c.

◆ Kmax

#define Kmax   7

Definition at line 524 of file dtoa.c.

◆ kshift

#define kshift   5

Definition at line 1643 of file dtoa.c.

◆ Llong

#define Llong   long long

Definition at line 512 of file dtoa.c.

◆ Log2P

#define Log2P   1

Definition at line 453 of file dtoa.c.

◆ Long

#define Long   long

Definition at line 190 of file dtoa.c.

◆ LSB

#define LSB   0x10000

Definition at line 451 of file dtoa.c.

◆ MALLOC

#define MALLOC   malloc

Definition at line 221 of file dtoa.c.

◆ n_bigtens

#define n_bigtens   2

Definition at line 1481 of file dtoa.c.

◆ Nbits

#define Nbits   56

Definition at line 438 of file dtoa.c.

◆ Need_Hexdig

#define Need_Hexdig

Definition at line 1494 of file dtoa.c.

◆ NO_STRTOD_BIGCOMP

#define NO_STRTOD_BIGCOMP

Definition at line 248 of file dtoa.c.

◆ P

#define P   56

Definition at line 437 of file dtoa.c.

◆ Pack_32

#define Pack_32

Definition at line 487 of file dtoa.c.

◆ PRIVATE_MEM

#define PRIVATE_MEM   2304

Definition at line 226 of file dtoa.c.

◆ PRIVATE_mem

#define PRIVATE_mem   ((PRIVATE_MEM+sizeof(double)-1)/sizeof(double))

Definition at line 228 of file dtoa.c.

◆ Quick_max

#define Quick_max   15

Definition at line 456 of file dtoa.c.

◆ ROUND_BIASED

#define ROUND_BIASED

Definition at line 462 of file dtoa.c.

◆ rounded_product

#define rounded_product ( a,
b )
Value:
a *= b
a
const GenericPointer< typename T::ValueType > T2 T::AllocatorType & a
Definition pointer.h:1181

Definition at line 479 of file dtoa.c.

◆ rounded_quotient

#define rounded_quotient ( a,
b )
Value:
a /= b

Definition at line 480 of file dtoa.c.

◆ Sign_bit

#define Sign_bit   0x8000

Definition at line 452 of file dtoa.c.

◆ Storeinc

#define Storeinc ( a,
b,
c )
Value:
(((unsigned short *)a)[0] = (unsigned short)b, \
((unsigned short *)a)[1] = (unsigned short)c, a++)

Definition at line 335 of file dtoa.c.

335#define Storeinc(a,b,c) (((unsigned short *)a)[0] = (unsigned short)b, \
336((unsigned short *)a)[1] = (unsigned short)c, a++)

◆ STRTOD_DIGLIM

#define STRTOD_DIGLIM   40

Definition at line 318 of file dtoa.c.

◆ strtod_diglim

#define strtod_diglim   STRTOD_DIGLIM

Definition at line 324 of file dtoa.c.

◆ Sudden_Underflow

#define Sudden_Underflow

Definition at line 399 of file dtoa.c.

◆ Ten_pmax

#define Ten_pmax   24

Definition at line 447 of file dtoa.c.

◆ Tiny0

#define Tiny0   0x80

Definition at line 454 of file dtoa.c.

◆ Tiny1

#define Tiny1   0

Definition at line 455 of file dtoa.c.

◆ ULbits

#define ULbits   32

Definition at line 1642 of file dtoa.c.

◆ ULLong

#define ULLong   unsigned Llong

Definition at line 515 of file dtoa.c.

◆ word0

#define word0 ( x)
Value:
(x)->L[0]

Definition at line 312 of file dtoa.c.

◆ word1

#define word1 ( x)
Value:
(x)->L[1]

Definition at line 313 of file dtoa.c.

Typedef Documentation

◆ BCinfo

typedef struct BCinfo BCinfo

Definition at line 490 of file dtoa.c.

◆ Bigint

typedef struct Bigint Bigint

Definition at line 539 of file dtoa.c.

◆ ULong

typedef unsigned Long ULong

Definition at line 193 of file dtoa.c.

Enumeration Type Documentation

◆ anonymous enum

anonymous enum
Enumerator
Round_zero 
Round_near 
Round_up 
Round_down 

Definition at line 1750 of file dtoa.c.

1750 { /* rounding values: same as FLT_ROUNDS */
1751 Round_zero = 0,
1752 Round_near = 1,
1753 Round_up = 2,
1754 Round_down = 3
1755 };
Round_zero
@ Round_zero
Definition dtoa.c:1751
Round_up
@ Round_up
Definition dtoa.c:1753
Round_near
@ Round_near
Definition dtoa.c:1752
Round_down
@ Round_down
Definition dtoa.c:1754

Function Documentation

◆ dtoa()

char * dtoa ( double dd,
int mode,
int ndigits,
int * decpt,
int * sign,
char ** rve )

Definition at line 3660 of file dtoa.c.

3667{
3668 /* Arguments ndigits, decpt, sign are similar to those
3669 of ecvt and fcvt; trailing zeros are suppressed from
3670 the returned string. If not null, *rve is set to point
3671 to the end of the return value. If d is +-Infinity or NaN,
3672 then *decpt is set to 9999.
3673
3674 mode:
3675 0 ==> shortest string that yields d when read in
3676 and rounded to nearest.
3677 1 ==> like 0, but with Steele & White stopping rule;
3678 e.g. with IEEE P754 arithmetic , mode 0 gives
3679 1e23 whereas mode 1 gives 9.999999999999999e22.
3680 2 ==> max(1,ndigits) significant digits. This gives a
3681 return value similar to that of ecvt, except
3682 that trailing zeros are suppressed.
3683 3 ==> through ndigits past the decimal point. This
3684 gives a return value similar to that from fcvt,
3685 except that trailing zeros are suppressed, and
3686 ndigits can be negative.
3687 4,5 ==> similar to 2 and 3, respectively, but (in
3688 round-nearest mode) with the tests of mode 0 to
3689 possibly return a shorter string that rounds to d.
3690 With IEEE arithmetic and compilation with
3691 -DHonor_FLT_ROUNDS, modes 4 and 5 behave the same
3692 as modes 2 and 3 when FLT_ROUNDS != 1.
3693 6-9 ==> Debugging modes similar to mode - 4: don't try
3694 fast floating-point estimate (if applicable).
3695
3696 Values of mode other than 0-9 are treated as mode 0.
3697
3698 Sufficient space is allocated to the return value
3699 to hold the suppressed trailing zeros.
3700 */
3701
3702 int bbits, b2, b5, be, dig, i, ieps, ilim, ilim0, ilim1,
3703 j, j1, k, k0, k_check, leftright, m2, m5, s2, s5,
3704 spec_case, try_quick;
3705 Long L;
3706#ifndef Sudden_Underflow
3707 int denorm;
3708 ULong x;
3709#endif
3710 Bigint *b, *b1, *delta, *mlo, *mhi, *S;
3711 U d2, eps, u;
3712 double ds;
3713 char *s, *s0;
3714#ifndef No_leftright
3715#ifdef IEEE_Arith
3716 U eps1;
3717#endif
3718#endif
3719#ifdef SET_INEXACT
3720 int inexact, oldinexact;
3721#endif
3722#ifdef Honor_FLT_ROUNDS /*{*/
3723 int Rounding;
3724#ifdef Trust_FLT_ROUNDS /*{{ only define this if FLT_ROUNDS really works! */
3725 Rounding = Flt_Rounds;
3726#else /*}{*/
3727 Rounding = 1;
3728 switch(fegetround()) {
3729 case FE_TOWARDZERO: Rounding = 0; break;
3730 case FE_UPWARD: Rounding = 2; break;
3731 case FE_DOWNWARD: Rounding = 3;
3732 }
3733#endif /*}}*/
3734#endif /*}*/
3735
3736#ifndef MULTIPLE_THREADS
3737 if (dtoa_result) {
3738 freedtoa(dtoa_result);
3739 dtoa_result = 0;
3740 }
3741#endif
3742
3743 u.d = dd;
3744 if (word0(&u) & Sign_bit) {
3745 /* set sign for everything, including 0's and NaNs */
3746 *sign = 1;
3747 word0(&u) &= ~Sign_bit; /* clear sign bit */
3748 }
3749 else
3750 *sign = 0;
3751
3752#if defined(IEEE_Arith) + defined(VAX)
3753#ifdef IEEE_Arith
3754 if ((word0(&u) & Exp_mask) == Exp_mask)
3755#else
3756 if (word0(&u) == 0x8000)
3757#endif
3758 {
3759 /* Infinity or NaN */
3760 *decpt = 9999;
3761#ifdef IEEE_Arith
3762 if (!word1(&u) && !(word0(&u) & 0xfffff))
3763 return nrv_alloc("Infinity", rve, 8);
3764#endif
3765 return nrv_alloc("NaN", rve, 3);
3766 }
3767#endif
3768#ifdef IBM
3769 dval(&u) += 0; /* normalize */
3770#endif
3771 if (!dval(&u)) {
3772 *decpt = 1;
3773 return nrv_alloc("0", rve, 1);
3774 }
3775
3776#ifdef SET_INEXACT
3777 try_quick = oldinexact = get_inexact();
3778 inexact = 1;
3779#endif
3780#ifdef Honor_FLT_ROUNDS
3781 if (Rounding >= 2) {
3782 if (*sign)
3783 Rounding = Rounding == 2 ? 0 : 2;
3784 else
3785 if (Rounding != 2)
3786 Rounding = 0;
3787 }
3788#endif
3789
3790 b = d2b(&u, &be, &bbits);
3791#ifdef Sudden_Underflow
3792 i = (int)(word0(&u) >> Exp_shift1 & (Exp_mask>>Exp_shift1));
3793#else
3794 if ((i = (int)(word0(&u) >> Exp_shift1 & (Exp_mask>>Exp_shift1)))) {
3795#endif
3796 dval(&d2) = dval(&u);
3797 word0(&d2) &= Frac_mask1;
3798 word0(&d2) |= Exp_11;
3799#ifdef IBM
3800 if (j = 11 - hi0bits(word0(&d2) & Frac_mask))
3801 dval(&d2) /= 1 << j;
3802#endif
3803
3804 /* log(x) ~=~ log(1.5) + (x-1.5)/1.5
3805 * log10(x) = log(x) / log(10)
3806 * ~=~ log(1.5)/log(10) + (x-1.5)/(1.5*log(10))
3807 * log10(d) = (i-Bias)*log(2)/log(10) + log10(d2)
3808 *
3809 * This suggests computing an approximation k to log10(d) by
3810 *
3811 * k = (i - Bias)*0.301029995663981
3812 * + ( (d2-1.5)*0.289529654602168 + 0.176091259055681 );
3813 *
3814 * We want k to be too large rather than too small.
3815 * The error in the first-order Taylor series approximation
3816 * is in our favor, so we just round up the constant enough
3817 * to compensate for any error in the multiplication of
3818 * (i - Bias) by 0.301029995663981; since |i - Bias| <= 1077,
3819 * and 1077 * 0.30103 * 2^-52 ~=~ 7.2e-14,
3820 * adding 1e-13 to the constant term more than suffices.
3821 * Hence we adjust the constant term to 0.1760912590558.
3822 * (We could get a more accurate k by invoking log10,
3823 * but this is probably not worthwhile.)
3824 */
3825
3826 i -= Bias;
3827#ifdef IBM
3828 i <<= 2;
3829 i += j;
3830#endif
3831#ifndef Sudden_Underflow
3832 denorm = 0;
3833 }
3834 else {
3835 /* d is denormalized */
3836
3837 i = bbits + be + (Bias + (P-1) - 1);
3838 x = i > 32 ? word0(&u) << (64 - i) | word1(&u) >> (i - 32)
3839 : word1(&u) << (32 - i);
3840 dval(&d2) = x;
3841 word0(&d2) -= 31*Exp_msk1; /* adjust exponent */
3842 i -= (Bias + (P-1) - 1) + 1;
3843 denorm = 1;
3844 }
3845#endif
3846 ds = (dval(&d2)-1.5)*0.289529654602168 + 0.1760912590558 + i*0.301029995663981;
3847 k = (int)ds;
3848 if (ds < 0. && ds != k)
3849 k--; /* want k = floor(ds) */
3850 k_check = 1;
3851 if (k >= 0 && k <= Ten_pmax) {
3852 if (dval(&u) < tens[k])
3853 k--;
3854 k_check = 0;
3855 }
3856 j = bbits - i - 1;
3857 if (j >= 0) {
3858 b2 = 0;
3859 s2 = j;
3860 }
3861 else {
3862 b2 = -j;
3863 s2 = 0;
3864 }
3865 if (k >= 0) {
3866 b5 = 0;
3867 s5 = k;
3868 s2 += k;
3869 }
3870 else {
3871 b2 -= k;
3872 b5 = -k;
3873 s5 = 0;
3874 }
3875 if (mode < 0 || mode > 9)
3876 mode = 0;
3877
3878#ifndef SET_INEXACT
3879#ifdef Check_FLT_ROUNDS
3880 try_quick = Rounding == 1;
3881#else
3882 try_quick = 1;
3883#endif
3884#endif /*SET_INEXACT*/
3885
3886 if (mode > 5) {
3887 mode -= 4;
3888 try_quick = 0;
3889 }
3890 leftright = 1;
3891 ilim = ilim1 = -1; /* Values for cases 0 and 1; done here to */
3892 /* silence erroneous "gcc -Wall" warning. */
3893 switch(mode) {
3894 case 0:
3895 case 1:
3896 i = 18;
3897 ndigits = 0;
3898 break;
3899 case 2:
3900 leftright = 0;
3901 /* no break */
3902 case 4:
3903 if (ndigits <= 0)
3904 ndigits = 1;
3905 ilim = ilim1 = i = ndigits;
3906 break;
3907 case 3:
3908 leftright = 0;
3909 /* no break */
3910 case 5:
3911 i = ndigits + k + 1;
3912 ilim = i;
3913 ilim1 = i - 1;
3914 if (i <= 0)
3915 i = 1;
3916 }
3917 s = s0 = rv_alloc(i);
3918
3919#ifdef Honor_FLT_ROUNDS
3920 if (mode > 1 && Rounding != 1)
3921 leftright = 0;
3922#endif
3923
3924 if (ilim >= 0 && ilim <= Quick_max && try_quick) {
3925
3926 /* Try to get by with floating-point arithmetic. */
3927
3928 i = 0;
3929 dval(&d2) = dval(&u);
3930 k0 = k;
3931 ilim0 = ilim;
3932 ieps = 2; /* conservative */
3933 if (k > 0) {
3934 ds = tens[k&0xf];
3935 j = k >> 4;
3936 if (j & Bletch) {
3937 /* prevent overflows */
3938 j &= Bletch - 1;
3939 dval(&u) /= bigtens[n_bigtens-1];
3940 ieps++;
3941 }
3942 for(; j; j >>= 1, i++)
3943 if (j & 1) {
3944 ieps++;
3945 ds *= bigtens[i];
3946 }
3947 dval(&u) /= ds;
3948 }
3949 else if ((j1 = -k)) {
3950 dval(&u) *= tens[j1 & 0xf];
3951 for(j = j1 >> 4; j; j >>= 1, i++)
3952 if (j & 1) {
3953 ieps++;
3954 dval(&u) *= bigtens[i];
3955 }
3956 }
3957 if (k_check && dval(&u) < 1. && ilim > 0) {
3958 if (ilim1 <= 0)
3959 goto fast_failed;
3960 ilim = ilim1;
3961 k--;
3962 dval(&u) *= 10.;
3963 ieps++;
3964 }
3965 dval(&eps) = ieps*dval(&u) + 7.;
3966 word0(&eps) -= (P-1)*Exp_msk1;
3967 if (ilim == 0) {
3968 S = mhi = 0;
3969 dval(&u) -= 5.;
3970 if (dval(&u) > dval(&eps))
3971 goto one_digit;
3972 if (dval(&u) < -dval(&eps))
3973 goto no_digits;
3974 goto fast_failed;
3975 }
3976#ifndef No_leftright
3977 if (leftright) {
3978 /* Use Steele & White method of only
3979 * generating digits needed.
3980 */
3981 dval(&eps) = 0.5/tens[ilim-1] - dval(&eps);
3982#ifdef IEEE_Arith
3983 if (k0 < 0 && j1 >= 307) {
3984 eps1.d = 1.01e256; /* 1.01 allows roundoff in the next few lines */
3985 word0(&eps1) -= Exp_msk1 * (Bias+P-1);
3986 dval(&eps1) *= tens[j1 & 0xf];
3987 for(i = 0, j = (j1-256) >> 4; j; j >>= 1, i++)
3988 if (j & 1)
3989 dval(&eps1) *= bigtens[i];
3990 if (eps.d < eps1.d)
3991 eps.d = eps1.d;
3992 }
3993#endif
3994 for(i = 0;;) {
3995 L = dval(&u);
3996 dval(&u) -= L;
3997 *s++ = '0' + (int)L;
3998 if (1. - dval(&u) < dval(&eps))
3999 goto bump_up;
4000 if (dval(&u) < dval(&eps))
4001 goto ret1;
4002 if (++i >= ilim)
4003 break;
4004 dval(&eps) *= 10.;
4005 dval(&u) *= 10.;
4006 }
4007 }
4008 else {
4009#endif
4010 /* Generate ilim digits, then fix them up. */
4011 dval(&eps) *= tens[ilim-1];
4012 for(i = 1;; i++, dval(&u) *= 10.) {
4013 L = (Long)(dval(&u));
4014 if (!(dval(&u) -= L))
4015 ilim = i;
4016 *s++ = '0' + (int)L;
4017 if (i == ilim) {
4018 if (dval(&u) > 0.5 + dval(&eps))
4019 goto bump_up;
4020 else if (dval(&u) < 0.5 - dval(&eps)) {
4021 while(*--s == '0');
4022 s++;
4023 goto ret1;
4024 }
4025 break;
4026 }
4027 }
4028#ifndef No_leftright
4029 }
4030#endif
4031 fast_failed:
4032 s = s0;
4033 dval(&u) = dval(&d2);
4034 k = k0;
4035 ilim = ilim0;
4036 }
4037
4038 /* Do we have a "small" integer? */
4039
4040 if (be >= 0 && k <= Int_max) {
4041 /* Yes. */
4042 ds = tens[k];
4043 if (ndigits < 0 && ilim <= 0) {
4044 S = mhi = 0;
4045 if (ilim < 0 || dval(&u) <= 5*ds)
4046 goto no_digits;
4047 goto one_digit;
4048 }
4049 for(i = 1;; i++, dval(&u) *= 10.) {
4050 L = (Long)(dval(&u) / ds);
4051 dval(&u) -= L*ds;
4052#ifdef Check_FLT_ROUNDS
4053 /* If FLT_ROUNDS == 2, L will usually be high by 1 */
4054 if (dval(&u) < 0) {
4055 L--;
4056 dval(&u) += ds;
4057 }
4058#endif
4059 *s++ = '0' + (int)L;
4060 if (!dval(&u)) {
4061#ifdef SET_INEXACT
4062 inexact = 0;
4063#endif
4064 break;
4065 }
4066 if (i == ilim) {
4067#ifdef Honor_FLT_ROUNDS
4068 if (mode > 1)
4069 switch(Rounding) {
4070 case 0: goto ret1;
4071 case 2: goto bump_up;
4072 }
4073#endif
4074 dval(&u) += dval(&u);
4075#ifdef ROUND_BIASED
4076 if (dval(&u) >= ds)
4077#else
4078 if (dval(&u) > ds || (dval(&u) == ds && L & 1))
4079#endif
4080 {
4081 bump_up:
4082 while(*--s == '9')
4083 if (s == s0) {
4084 k++;
4085 *s = '0';
4086 break;
4087 }
4088 ++*s++;
4089 }
4090 break;
4091 }
4092 }
4093 goto ret1;
4094 }
4095
4096 m2 = b2;
4097 m5 = b5;
4098 mhi = mlo = 0;
4099 if (leftright) {
4100 i =
4101#ifndef Sudden_Underflow
4102 denorm ? be + (Bias + (P-1) - 1 + 1) :
4103#endif
4104#ifdef IBM
4105 1 + 4*P - 3 - bbits + ((bbits + be - 1) & 3);
4106#else
4107 1 + P - bbits;
4108#endif
4109 b2 += i;
4110 s2 += i;
4111 mhi = i2b(1);
4112 }
4113 if (m2 > 0 && s2 > 0) {
4114 i = m2 < s2 ? m2 : s2;
4115 b2 -= i;
4116 m2 -= i;
4117 s2 -= i;
4118 }
4119 if (b5 > 0) {
4120 if (leftright) {
4121 if (m5 > 0) {
4122 mhi = pow5mult(mhi, m5);
4123 b1 = mult(mhi, b);
4124 Bfree(b);
4125 b = b1;
4126 }
4127 if ((j = b5 - m5))
4128 b = pow5mult(b, j);
4129 }
4130 else
4131 b = pow5mult(b, b5);
4132 }
4133 S = i2b(1);
4134 if (s5 > 0)
4135 S = pow5mult(S, s5);
4136
4137 /* Check for special case that d is a normalized power of 2. */
4138
4139 spec_case = 0;
4140 if ((mode < 2 || leftright)
4141#ifdef Honor_FLT_ROUNDS
4142 && Rounding == 1
4143#endif
4144 ) {
4145 if (!word1(&u) && !(word0(&u) & Bndry_mask)
4146#ifndef Sudden_Underflow
4147 && word0(&u) & (Exp_mask & ~Exp_msk1)
4148#endif
4149 ) {
4150 /* The special case */
4151 b2 += Log2P;
4152 s2 += Log2P;
4153 spec_case = 1;
4154 }
4155 }
4156
4157 /* Arrange for convenient computation of quotients:
4158 * shift left if necessary so divisor has 4 leading 0 bits.
4159 *
4160 * Perhaps we should just compute leading 28 bits of S once
4161 * and for all and pass them and a shift to quorem, so it
4162 * can do shifts and ors to compute the numerator for q.
4163 */
4164 i = dshift(S, s2);
4165 b2 += i;
4166 m2 += i;
4167 s2 += i;
4168 if (b2 > 0)
4169 b = lshift(b, b2);
4170 if (s2 > 0)
4171 S = lshift(S, s2);
4172 if (k_check) {
4173 if (cmp(b,S) < 0) {
4174 k--;
4175 b = multadd(b, 10, 0); /* we botched the k estimate */
4176 if (leftright)
4177 mhi = multadd(mhi, 10, 0);
4178 ilim = ilim1;
4179 }
4180 }
4181 if (ilim <= 0 && (mode == 3 || mode == 5)) {
4182 if (ilim < 0 || cmp(b,S = multadd(S,5,0)) <= 0) {
4183 /* no digits, fcvt style */
4184 no_digits:
4185 k = -1 - ndigits;
4186 goto ret;
4187 }
4188 one_digit:
4189 *s++ = '1';
4190 k++;
4191 goto ret;
4192 }
4193 if (leftright) {
4194 if (m2 > 0)
4195 mhi = lshift(mhi, m2);
4196
4197 /* Compute mlo -- check for special case
4198 * that d is a normalized power of 2.
4199 */
4200
4201 mlo = mhi;
4202 if (spec_case) {
4203 mhi = Balloc(mhi->k);
4204 Bcopy(mhi, mlo);
4205 mhi = lshift(mhi, Log2P);
4206 }
4207
4208 for(i = 1;;i++) {
4209 dig = quorem(b,S) + '0';
4210 /* Do we yet have the shortest decimal string
4211 * that will round to d?
4212 */
4213 j = cmp(b, mlo);
4214 delta = diff(S, mhi);
4215 j1 = delta->sign ? 1 : cmp(b, delta);
4216 Bfree(delta);
4217#ifndef ROUND_BIASED
4218 if (j1 == 0 && mode != 1 && !(word1(&u) & 1)
4219#ifdef Honor_FLT_ROUNDS
4220 && Rounding >= 1
4221#endif
4222 ) {
4223 if (dig == '9')
4224 goto round_9_up;
4225 if (j > 0)
4226 dig++;
4227#ifdef SET_INEXACT
4228 else if (!b->x[0] && b->wds <= 1)
4229 inexact = 0;
4230#endif
4231 *s++ = dig;
4232 goto ret;
4233 }
4234#endif
4235 if (j < 0 || (j == 0 && mode != 1
4236#ifndef ROUND_BIASED
4237 && !(word1(&u) & 1)
4238#endif
4239 )) {
4240 if (!b->x[0] && b->wds <= 1) {
4241#ifdef SET_INEXACT
4242 inexact = 0;
4243#endif
4244 goto accept_dig;
4245 }
4246#ifdef Honor_FLT_ROUNDS
4247 if (mode > 1)
4248 switch(Rounding) {
4249 case 0: goto accept_dig;
4250 case 2: goto keep_dig;
4251 }
4252#endif /*Honor_FLT_ROUNDS*/
4253 if (j1 > 0) {
4254 b = lshift(b, 1);
4255 j1 = cmp(b, S);
4256#ifdef ROUND_BIASED
4257 if (j1 >= 0 /*)*/
4258#else
4259 if ((j1 > 0 || (j1 == 0 && dig & 1))
4260#endif
4261 && dig++ == '9')
4262 goto round_9_up;
4263 }
4264 accept_dig:
4265 *s++ = dig;
4266 goto ret;
4267 }
4268 if (j1 > 0) {
4269#ifdef Honor_FLT_ROUNDS
4270 if (!Rounding)
4271 goto accept_dig;
4272#endif
4273 if (dig == '9') { /* possible if i == 1 */
4274 round_9_up:
4275 *s++ = '9';
4276 goto roundoff;
4277 }
4278 *s++ = dig + 1;
4279 goto ret;
4280 }
4281#ifdef Honor_FLT_ROUNDS
4282 keep_dig:
4283#endif
4284 *s++ = dig;
4285 if (i == ilim)
4286 break;
4287 b = multadd(b, 10, 0);
4288 if (mlo == mhi)
4289 mlo = mhi = multadd(mhi, 10, 0);
4290 else {
4291 mlo = multadd(mlo, 10, 0);
4292 mhi = multadd(mhi, 10, 0);
4293 }
4294 }
4295 }
4296 else
4297 for(i = 1;; i++) {
4298 *s++ = dig = quorem(b,S) + '0';
4299 if (!b->x[0] && b->wds <= 1) {
4300#ifdef SET_INEXACT
4301 inexact = 0;
4302#endif
4303 goto ret;
4304 }
4305 if (i >= ilim)
4306 break;
4307 b = multadd(b, 10, 0);
4308 }
4309
4310 /* Round off last digit */
4311
4312#ifdef Honor_FLT_ROUNDS
4313 switch(Rounding) {
4314 case 0: goto trimzeros;
4315 case 2: goto roundoff;
4316 }
4317#endif
4318 b = lshift(b, 1);
4319 j = cmp(b, S);
4320#ifdef ROUND_BIASED
4321 if (j >= 0)
4322#else
4323 if (j > 0 || (j == 0 && dig & 1))
4324#endif
4325 {
4326 roundoff:
4327 while(*--s == '9')
4328 if (s == s0) {
4329 k++;
4330 *s++ = '1';
4331 goto ret;
4332 }
4333 ++*s++;
4334 }
4335 else {
4336#ifdef Honor_FLT_ROUNDS
4337 trimzeros:
4338#endif
4339 while(*--s == '0');
4340 s++;
4341 }
4342 ret:
4343 Bfree(S);
4344 if (mhi) {
4345 if (mlo && mlo != mhi)
4346 Bfree(mlo);
4347 Bfree(mhi);
4348 }
4349 ret1:
4350#ifdef SET_INEXACT
4351 if (inexact) {
4352 if (!oldinexact) {
4353 word0(&u) = Exp_1 + (70 << Exp_shift);
4354 word1(&u) = 0;
4355 dval(&u) += 1.;
4356 }
4357 }
4358 else if (!oldinexact)
4359 clear_inexact();
4360#endif
4361 Bfree(b);
4362 *s = 0;
4363 *decpt = k + 1;
4364 if (rve)
4365 *rve = s;
4366 return s0;
4367 }
freedtoa
void freedtoa(char *s)
Definition dtoa.c:3613
Exp_shift
#define Exp_shift
Definition dtoa.c:432
Exp_msk1
#define Exp_msk1
Definition dtoa.c:434
P
#define P
Definition dtoa.c:437
Bndry_mask
#define Bndry_mask
Definition dtoa.c:449
word1
#define word1(x)
Definition dtoa.c:313
Frac_mask
#define Frac_mask
Definition dtoa.c:445
Frac_mask1
#define Frac_mask1
Definition dtoa.c:446
Quick_max
#define Quick_max
Definition dtoa.c:456
Bias
#define Bias
Definition dtoa.c:439
n_bigtens
#define n_bigtens
Definition dtoa.c:1481
dval
#define dval(x)
Definition dtoa.c:315
Exp_mask
#define Exp_mask
Definition dtoa.c:436
Ten_pmax
#define Ten_pmax
Definition dtoa.c:447
Sign_bit
#define Sign_bit
Definition dtoa.c:452
Bletch
#define Bletch
Definition dtoa.c:448
Flt_Rounds
#define Flt_Rounds
Definition dtoa.c:431
word0
#define word0(x)
Definition dtoa.c:312
Exp_1
#define Exp_1
Definition dtoa.c:442
Exp_shift1
#define Exp_shift1
Definition dtoa.c:433
Sudden_Underflow
#define Sudden_Underflow
Definition dtoa.c:399
Bcopy
#define Bcopy(x, y)
Definition dtoa.c:608
ROUND_BIASED
#define ROUND_BIASED
Definition dtoa.c:462
Log2P
#define Log2P
Definition dtoa.c:453
Exp_11
#define Exp_11
Definition dtoa.c:443
Int_max
#define Int_max
Definition dtoa.c:457
ULong
unsigned Long ULong
Definition dtoa.c:193
diff
void diff(const std::string &a, const std::string &b)
Definition jmp.cpp:18
Xbyak::util::ds
static const Segment ds(Segment::ds)
S
#define S(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p)
Definition precomputed_ecmult.c:12
Bigint
Definition dtoa.c:533
Bigint::k
int k
Definition dtoa.c:535
Bigint::sign
int sign
Definition dtoa.c:535
Bigint::wds
int wds
Definition dtoa.c:535
Bigint::x
ULong x[1]
Definition dtoa.c:536
U
Definition dtoa.c:306
U::d
double d
Definition dtoa.c:306
cmp
void cmp(const Operand &op, uint32 imm)
Definition xbyak_mnemonic.h:93
ret
CK_RV ret
Definition yubihsm_pkcs11.c:973
s
char * s
Definition yubihsm_pkcs11.c:524
j
uint16_t j
Definition yubihsm_pkcs11.c:465
Here is the call graph for this function:

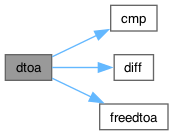
◆ freedtoa()

void freedtoa ( char * s)

Definition at line 3613 of file dtoa.c.

3615{
3616 Bigint *b = (Bigint *)((int *)s - 1);
3617 b->maxwds = 1 << (b->k = *(int*)b);
3618 Bfree(b);
3619#ifndef MULTIPLE_THREADS
3620 if (s == dtoa_result)
3621 dtoa_result = 0;
3622#endif
3623 }
Bigint::maxwds
int maxwds
Definition dtoa.c:535
Here is the caller graph for this function:

◆ gethex()

void gethex ( CONST char ** sp,
U * rvp,
int rounding,
int sign )

Definition at line 1762 of file dtoa.c.

1764{
1765 Bigint *b;
1766 CONST unsigned char *decpt, *s0, *s, *s1;
1767 Long e, e1;
1768 ULong L, lostbits, *x;
1769 int big, denorm, esign, havedig, k, n, nbits, up, zret;
1770#ifdef IBM
1771 int j;
1772#endif
1773 enum {
1774#ifdef IEEE_Arith /*{{*/
1775 emax = 0x7fe - Bias - P + 1,
1776 emin = Emin - P + 1
1777#else /*}{*/
1778 emin = Emin - P,
1779#ifdef VAX
1780 emax = 0x7ff - Bias - P + 1
1781#endif
1782#ifdef IBM
1783 emax = 0x7f - Bias - P
1784#endif
1785#endif /*}}*/
1786 };
1787#ifdef USE_LOCALE
1788 int i;
1789#ifdef NO_LOCALE_CACHE
1790 const unsigned char *decimalpoint = (unsigned char*)
1791 localeconv()->decimal_point;
1792#else
1793 const unsigned char *decimalpoint;
1794 static unsigned char *decimalpoint_cache;
1795 if (!(s0 = decimalpoint_cache)) {
1796 s0 = (unsigned char*)localeconv()->decimal_point;
1797 if ((decimalpoint_cache = (unsigned char*)
1798 MALLOC(strlen((CONST char*)s0) + 1))) {
1799 strcpy((char*)decimalpoint_cache, (CONST char*)s0);
1800 s0 = decimalpoint_cache;
1801 }
1802 }
1803 decimalpoint = s0;
1804#endif
1805#endif
1806
1807 /**** if (!hexdig['0']) hexdig_init(); ****/
1808 havedig = 0;
1809 s0 = *(CONST unsigned char **)sp + 2;
1810 while(s0[havedig] == '0')
1811 havedig++;
1812 s0 += havedig;
1813 s = s0;
1814 decpt = 0;
1815 zret = 0;
1816 e = 0;
1817 if (hexdig[*s])
1818 havedig++;
1819 else {
1820 zret = 1;
1821#ifdef USE_LOCALE
1822 for(i = 0; decimalpoint[i]; ++i) {
1823 if (s[i] != decimalpoint[i])
1824 goto pcheck;
1825 }
1826 decpt = s += i;
1827#else
1828 if (*s != '.')
1829 goto pcheck;
1830 decpt = ++s;
1831#endif
1832 if (!hexdig[*s])
1833 goto pcheck;
1834 while(*s == '0')
1835 s++;
1836 if (hexdig[*s])
1837 zret = 0;
1838 havedig = 1;
1839 s0 = s;
1840 }
1841 while(hexdig[*s])
1842 s++;
1843#ifdef USE_LOCALE
1844 if (*s == *decimalpoint && !decpt) {
1845 for(i = 1; decimalpoint[i]; ++i) {
1846 if (s[i] != decimalpoint[i])
1847 goto pcheck;
1848 }
1849 decpt = s += i;
1850#else
1851 if (*s == '.' && !decpt) {
1852 decpt = ++s;
1853#endif
1854 while(hexdig[*s])
1855 s++;
1856 }/*}*/
1857 if (decpt)
1858 e = -(((Long)(s-decpt)) << 2);
1859 pcheck:
1860 s1 = s;
1861 big = esign = 0;
1862 switch(*s) {
1863 case 'p':
1864 case 'P':
1865 switch(*++s) {
1866 case '-':
1867 esign = 1;
1868 /* no break */
1869 case '+':
1870 s++;
1871 }
1872 if ((n = hexdig[*s]) == 0 || n > 0x19) {
1873 s = s1;
1874 break;
1875 }
1876 e1 = n - 0x10;
1877 while((n = hexdig[*++s]) !=0 && n <= 0x19) {
1878 if (e1 & 0xf8000000)
1879 big = 1;
1880 e1 = 10*e1 + n - 0x10;
1881 }
1882 if (esign)
1883 e1 = -e1;
1884 e += e1;
1885 }
1886 *sp = (char*)s;
1887 if (!havedig)
1888 *sp = (char*)s0 - 1;
1889 if (zret)
1890 goto retz1;
1891 if (big) {
1892 if (esign) {
1893#ifdef IEEE_Arith
1894 switch(rounding) {
1895 case Round_up:
1896 if (sign)
1897 break;
1898 goto ret_tiny;
1899 case Round_down:
1900 if (!sign)
1901 break;
1902 goto ret_tiny;
1903 }
1904#endif
1905 goto retz;
1906#ifdef IEEE_Arith
1907 ret_tinyf:
1908 Bfree(b);
1909 ret_tiny:
1910#ifndef NO_ERRNO
1911 errno = ERANGE;
1912#endif
1913 word0(rvp) = 0;
1914 word1(rvp) = 1;
1915 return;
1916#endif /* IEEE_Arith */
1917 }
1918 switch(rounding) {
1919 case Round_near:
1920 goto ovfl1;
1921 case Round_up:
1922 if (!sign)
1923 goto ovfl1;
1924 goto ret_big;
1925 case Round_down:
1926 if (sign)
1927 goto ovfl1;
1928 goto ret_big;
1929 }
1930 ret_big:
1931 word0(rvp) = Big0;
1932 word1(rvp) = Big1;
1933 return;
1934 }
1935 n = s1 - s0 - 1;
1936 for(k = 0; n > (1 << (kshift-2)) - 1; n >>= 1)
1937 k++;
1938 b = Balloc(k);
1939 x = b->x;
1940 n = 0;
1941 L = 0;
1942#ifdef USE_LOCALE
1943 for(i = 0; decimalpoint[i+1]; ++i);
1944#endif
1945 while(s1 > s0) {
1946#ifdef USE_LOCALE
1947 if (*--s1 == decimalpoint[i]) {
1948 s1 -= i;
1949 continue;
1950 }
1951#else
1952 if (*--s1 == '.')
1953 continue;
1954#endif
1955 if (n == ULbits) {
1956 *x++ = L;
1957 L = 0;
1958 n = 0;
1959 }
1960 L |= (hexdig[*s1] & 0x0f) << n;
1961 n += 4;
1962 }
1963 *x++ = L;
1964 b->wds = n = x - b->x;
1965 n = ULbits*n - hi0bits(L);
1966 nbits = Nbits;
1967 lostbits = 0;
1968 x = b->x;
1969 if (n > nbits) {
1970 n -= nbits;
1971 if (any_on(b,n)) {
1972 lostbits = 1;
1973 k = n - 1;
1974 if (x[k>>kshift] & 1 << (k & kmask)) {
1975 lostbits = 2;
1976 if (k > 0 && any_on(b,k))
1977 lostbits = 3;
1978 }
1979 }
1980 rshift(b, n);
1981 e += n;
1982 }
1983 else if (n < nbits) {
1984 n = nbits - n;
1985 b = lshift(b, n);
1986 e -= n;
1987 x = b->x;
1988 }
1989 if (e > Emax) {
1990 ovfl:
1991 Bfree(b);
1992 ovfl1:
1993#ifndef NO_ERRNO
1994 errno = ERANGE;
1995#endif
1996 word0(rvp) = Exp_mask;
1997 word1(rvp) = 0;
1998 return;
1999 }
2000 denorm = 0;
2001 if (e < emin) {
2002 denorm = 1;
2003 n = emin - e;
2004 if (n >= nbits) {
2005#ifdef IEEE_Arith /*{*/
2006 switch (rounding) {
2007 case Round_near:
2008 if (n == nbits && (n < 2 || any_on(b,n-1)))
2009 goto ret_tinyf;
2010 break;
2011 case Round_up:
2012 if (!sign)
2013 goto ret_tinyf;
2014 break;
2015 case Round_down:
2016 if (sign)
2017 goto ret_tinyf;
2018 }
2019#endif /* } IEEE_Arith */
2020 Bfree(b);
2021 retz:
2022#ifndef NO_ERRNO
2023 errno = ERANGE;
2024#endif
2025 retz1:
2026 rvp->d = 0.;
2027 return;
2028 }
2029 k = n - 1;
2030 if (lostbits)
2031 lostbits = 1;
2032 else if (k > 0)
2033 lostbits = any_on(b,k);
2034 if (x[k>>kshift] & 1 << (k & kmask))
2035 lostbits |= 2;
2036 nbits -= n;
2037 rshift(b,n);
2038 e = emin;
2039 }
2040 if (lostbits) {
2041 up = 0;
2042 switch(rounding) {
2043 case Round_zero:
2044 break;
2045 case Round_near:
2046 if (lostbits & 2
2047 && (lostbits & 1) | (x[0] & 1))
2048 up = 1;
2049 break;
2050 case Round_up:
2051 up = 1 - sign;
2052 break;
2053 case Round_down:
2054 up = sign;
2055 }
2056 if (up) {
2057 k = b->wds;
2058 b = increment(b);
2059 x = b->x;
2060 if (denorm) {
2061#if 0
2062 if (nbits == Nbits - 1
2063 && x[nbits >> kshift] & 1 << (nbits & kmask))
2064 denorm = 0; /* not currently used */
2065#endif
2066 }
2067 else if (b->wds > k
2068 || ((n = nbits & kmask) !=0
2069 && hi0bits(x[k-1]) < 32-n)) {
2070 rshift(b,1);
2071 if (++e > Emax)
2072 goto ovfl;
2073 }
2074 }
2075 }
2076#ifdef IEEE_Arith
2077 if (denorm)
2078 word0(rvp) = b->wds > 1 ? b->x[1] & ~0x100000 : 0;
2079 else
2080 word0(rvp) = (b->x[1] & ~0x100000) | ((e + 0x3ff + 52) << 20);
2081 word1(rvp) = b->x[0];
2082#endif
2083#ifdef IBM
2084 if ((j = e & 3)) {
2085 k = b->x[0] & ((1 << j) - 1);
2086 rshift(b,j);
2087 if (k) {
2088 switch(rounding) {
2089 case Round_up:
2090 if (!sign)
2091 increment(b);
2092 break;
2093 case Round_down:
2094 if (sign)
2095 increment(b);
2096 break;
2097 case Round_near:
2098 j = 1 << (j-1);
2099 if (k & j && ((k & (j-1)) | lostbits))
2100 increment(b);
2101 }
2102 }
2103 }
2104 e >>= 2;
2105 word0(rvp) = b->x[1] | ((e + 65 + 13) << 24);
2106 word1(rvp) = b->x[0];
2107#endif
2108#ifdef VAX
2109 /* The next two lines ignore swap of low- and high-order 2 bytes. */
2110 /* word0(rvp) = (b->x[1] & ~0x800000) | ((e + 129 + 55) << 23); */
2111 /* word1(rvp) = b->x[0]; */
2112 word0(rvp) = ((b->x[1] & ~0x800000) >> 16) | ((e + 129 + 55) << 7) | (b->x[1] << 16);
2113 word1(rvp) = (b->x[0] >> 16) | (b->x[0] << 16);
2114#endif
2115 Bfree(b);
2116 }
Emax
#define Emax
Definition dtoa.c:440
CONST
#define CONST
Definition dtoa.c:298
Big1
#define Big1
Definition dtoa.c:484
Nbits
#define Nbits
Definition dtoa.c:438
MALLOC
#define MALLOC
Definition dtoa.c:221
kmask
#define kmask
Definition dtoa.c:1644
kshift
#define kshift
Definition dtoa.c:1643
Emin
#define Emin
Definition dtoa.c:441
Big0
#define Big0
Definition dtoa.c:483
ULbits
#define ULbits
Definition dtoa.c:1642
Xbyak::util::sp
static const Reg16 sp(Operand::SP)
Here is the call graph for this function:
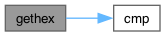
Here is the caller graph for this function:

◆ strtod()

double strtod ( const char * s00,
char ** se )

Definition at line 2489 of file dtoa.c.

2495{
2496 int bb2, bb5, bbe, bd2, bd5, bbbits, bs2, c, e, e1;
2497 int esign, i, j, k, nd, nd0, nf, nz, nz0, nz1, sign;
2498 CONST char *s, *s0, *s1;
2499 double aadj, aadj1;
2500 Long L;
2501 U aadj2, adj, rv, rv0;
2502 ULong y, z;
2503 BCinfo bc;
2504 Bigint *bb, *bb1, *bd, *bd0, *bs, *delta;
2505#ifdef Avoid_Underflow
2506 ULong Lsb, Lsb1;
2507#endif
2508#ifdef SET_INEXACT
2509 int oldinexact;
2510#endif
2511#ifndef NO_STRTOD_BIGCOMP
2512 int req_bigcomp = 0;
2513#endif
2514#ifdef Honor_FLT_ROUNDS /*{*/
2515#ifdef Trust_FLT_ROUNDS /*{{ only define this if FLT_ROUNDS really works! */
2516 bc.rounding = Flt_Rounds;
2517#else /*}{*/
2518 bc.rounding = 1;
2519 switch(fegetround()) {
2520 case FE_TOWARDZERO: bc.rounding = 0; break;
2521 case FE_UPWARD: bc.rounding = 2; break;
2522 case FE_DOWNWARD: bc.rounding = 3;
2523 }
2524#endif /*}}*/
2525#endif /*}*/
2526#ifdef USE_LOCALE
2527 CONST char *s2;
2528#endif
2529
2530 sign = nz0 = nz1 = nz = bc.dplen = bc.uflchk = 0;
2531 dval(&rv) = 0.;
2532 for(s = s00;;s++) switch(*s) {
2533 case '-':
2534 sign = 1;
2535 /* no break */
2536 case '+':
2537 if (*++s)
2538 goto break2;
2539 /* no break */
2540 case 0:
2541 goto ret0;
2542 case '\t':
2543 case '\n':
2544 case '\v':
2545 case '\f':
2546 case '\r':
2547 case ' ':
2548 continue;
2549 default:
2550 goto break2;
2551 }
2552 break2:
2553 if (*s == '0') {
2554#ifndef NO_HEX_FP /*{*/
2555 switch(s[1]) {
2556 case 'x':
2557 case 'X':
2558#ifdef Honor_FLT_ROUNDS
2559 gethex(&s, &rv, bc.rounding, sign);
2560#else
2561 gethex(&s, &rv, 1, sign);
2562#endif
2563 goto ret;
2564 }
2565#endif /*}*/
2566 nz0 = 1;
2567 while(*++s == '0') ;
2568 if (!*s)
2569 goto ret;
2570 }
2571 s0 = s;
2572 y = z = 0;
2573 for(nd = nf = 0; (c = *s) >= '0' && c <= '9'; nd++, s++)
2574 if (nd < 9)
2575 y = 10*y + c - '0';
2576 else if (nd < DBL_DIG + 2)
2577 z = 10*z + c - '0';
2578 nd0 = nd;
2579 bc.dp0 = bc.dp1 = s - s0;
2580 for(s1 = s; s1 > s0 && *--s1 == '0'; )
2581 ++nz1;
2582#ifdef USE_LOCALE
2583 s1 = localeconv()->decimal_point;
2584 if (c == *s1) {
2585 c = '.';
2586 if (*++s1) {
2587 s2 = s;
2588 for(;;) {
2589 if (*++s2 != *s1) {
2590 c = 0;
2591 break;
2592 }
2593 if (!*++s1) {
2594 s = s2;
2595 break;
2596 }
2597 }
2598 }
2599 }
2600#endif
2601 if (c == '.') {
2602 c = *++s;
2603 bc.dp1 = s - s0;
2604 bc.dplen = bc.dp1 - bc.dp0;
2605 if (!nd) {
2606 for(; c == '0'; c = *++s)
2607 nz++;
2608 if (c > '0' && c <= '9') {
2609 bc.dp0 = s0 - s;
2610 bc.dp1 = bc.dp0 + bc.dplen;
2611 s0 = s;
2612 nf += nz;
2613 nz = 0;
2614 goto have_dig;
2615 }
2616 goto dig_done;
2617 }
2618 for(; c >= '0' && c <= '9'; c = *++s) {
2619 have_dig:
2620 nz++;
2621 if (c -= '0') {
2622 nf += nz;
2623 for(i = 1; i < nz; i++)
2624 if (nd++ < 9)
2625 y *= 10;
2626 else if (nd <= DBL_DIG + 2)
2627 z *= 10;
2628 if (nd++ < 9)
2629 y = 10*y + c;
2630 else if (nd <= DBL_DIG + 2)
2631 z = 10*z + c;
2632 nz = nz1 = 0;
2633 }
2634 }
2635 }
2636 dig_done:
2637 e = 0;
2638 if (c == 'e' || c == 'E') {
2639 if (!nd && !nz && !nz0) {
2640 goto ret0;
2641 }
2642 s00 = s;
2643 esign = 0;
2644 switch(c = *++s) {
2645 case '-':
2646 esign = 1;
2647 case '+':
2648 c = *++s;
2649 }
2650 if (c >= '0' && c <= '9') {
2651 while(c == '0')
2652 c = *++s;
2653 if (c > '0' && c <= '9') {
2654 L = c - '0';
2655 s1 = s;
2656 while((c = *++s) >= '0' && c <= '9')
2657 L = 10*L + c - '0';
2658 if (s - s1 > 8 || L > 19999)
2659 /* Avoid confusion from exponents
2660 * so large that e might overflow.
2661 */
2662 e = 19999; /* safe for 16 bit ints */
2663 else
2664 e = (int)L;
2665 if (esign)
2666 e = -e;
2667 }
2668 else
2669 e = 0;
2670 }
2671 else
2672 s = s00;
2673 }
2674 if (!nd) {
2675 if (!nz && !nz0) {
2676#ifdef INFNAN_CHECK
2677 /* Check for Nan and Infinity */
2678 if (!bc.dplen)
2679 switch(c) {
2680 case 'i':
2681 case 'I':
2682 if (match(&s,"nf")) {
2683 --s;
2684 if (!match(&s,"inity"))
2685 ++s;
2686 word0(&rv) = 0x7ff00000;
2687 word1(&rv) = 0;
2688 goto ret;
2689 }
2690 break;
2691 case 'n':
2692 case 'N':
2693 if (match(&s, "an")) {
2694 word0(&rv) = NAN_WORD0;
2695 word1(&rv) = NAN_WORD1;
2696#ifndef No_Hex_NaN
2697 if (*s == '(') /*)*/
2698 hexnan(&rv, &s);
2699#endif
2700 goto ret;
2701 }
2702 }
2703#endif /* INFNAN_CHECK */
2704 ret0:
2705 s = s00;
2706 sign = 0;
2707 }
2708 goto ret;
2709 }
2710 bc.e0 = e1 = e -= nf;
2711
2712 /* Now we have nd0 digits, starting at s0, followed by a
2713 * decimal point, followed by nd-nd0 digits. The number we're
2714 * after is the integer represented by those digits times
2715 * 10**e */
2716
2717 if (!nd0)
2718 nd0 = nd;
2719 k = nd < DBL_DIG + 2 ? nd : DBL_DIG + 2;
2720 dval(&rv) = y;
2721 if (k > 9) {
2722#ifdef SET_INEXACT
2723 if (k > DBL_DIG)
2724 oldinexact = get_inexact();
2725#endif
2726 dval(&rv) = tens[k - 9] * dval(&rv) + z;
2727 }
2728 bd0 = 0;
2729 if (nd <= DBL_DIG
2730#ifndef RND_PRODQUOT
2731#ifndef Honor_FLT_ROUNDS
2732 && Flt_Rounds == 1
2733#endif
2734#endif
2735 ) {
2736 if (!e)
2737 goto ret;
2738#ifndef ROUND_BIASED_without_Round_Up
2739 if (e > 0) {
2740 if (e <= Ten_pmax) {
2741#ifdef VAX
2742 goto vax_ovfl_check;
2743#else
2744#ifdef Honor_FLT_ROUNDS
2745 /* round correctly FLT_ROUNDS = 2 or 3 */
2746 if (sign) {
2747 rv.d = -rv.d;
2748 sign = 0;
2749 }
2750#endif
2751 /* rv = */ rounded_product(dval(&rv), tens[e]);
2752 goto ret;
2753#endif
2754 }
2755 i = DBL_DIG - nd;
2756 if (e <= Ten_pmax + i) {
2757 /* A fancier test would sometimes let us do
2758 * this for larger i values.
2759 */
2760#ifdef Honor_FLT_ROUNDS
2761 /* round correctly FLT_ROUNDS = 2 or 3 */
2762 if (sign) {
2763 rv.d = -rv.d;
2764 sign = 0;
2765 }
2766#endif
2767 e -= i;
2768 dval(&rv) *= tens[i];
2769#ifdef VAX
2770 /* VAX exponent range is so narrow we must
2771 * worry about overflow here...
2772 */
2773 vax_ovfl_check:
2774 word0(&rv) -= P*Exp_msk1;
2775 /* rv = */ rounded_product(dval(&rv), tens[e]);
2776 if ((word0(&rv) & Exp_mask)
2777 > Exp_msk1*(DBL_MAX_EXP+Bias-1-P))
2778 goto ovfl;
2779 word0(&rv) += P*Exp_msk1;
2780#else
2781 /* rv = */ rounded_product(dval(&rv), tens[e]);
2782#endif
2783 goto ret;
2784 }
2785 }
2786#ifndef Inaccurate_Divide
2787 else if (e >= -Ten_pmax) {
2788#ifdef Honor_FLT_ROUNDS
2789 /* round correctly FLT_ROUNDS = 2 or 3 */
2790 if (sign) {
2791 rv.d = -rv.d;
2792 sign = 0;
2793 }
2794#endif
2795 /* rv = */ rounded_quotient(dval(&rv), tens[-e]);
2796 goto ret;
2797 }
2798#endif
2799#endif /* ROUND_BIASED_without_Round_Up */
2800 }
2801 e1 += nd - k;
2802
2803#ifdef IEEE_Arith
2804#ifdef SET_INEXACT
2805 bc.inexact = 1;
2806 if (k <= DBL_DIG)
2807 oldinexact = get_inexact();
2808#endif
2809#ifdef Avoid_Underflow
2810 bc.scale = 0;
2811#endif
2812#ifdef Honor_FLT_ROUNDS
2813 if (bc.rounding >= 2) {
2814 if (sign)
2815 bc.rounding = bc.rounding == 2 ? 0 : 2;
2816 else
2817 if (bc.rounding != 2)
2818 bc.rounding = 0;
2819 }
2820#endif
2821#endif /*IEEE_Arith*/
2822
2823 /* Get starting approximation = rv * 10**e1 */
2824
2825 if (e1 > 0) {
2826 if ((i = e1 & 15))
2827 dval(&rv) *= tens[i];
2828 if (e1 &= ~15) {
2829 if (e1 > DBL_MAX_10_EXP) {
2830 ovfl:
2831 /* Can't trust HUGE_VAL */
2832#ifdef IEEE_Arith
2833#ifdef Honor_FLT_ROUNDS
2834 switch(bc.rounding) {
2835 case 0: /* toward 0 */
2836 case 3: /* toward -infinity */
2837 word0(&rv) = Big0;
2838 word1(&rv) = Big1;
2839 break;
2840 default:
2841 word0(&rv) = Exp_mask;
2842 word1(&rv) = 0;
2843 }
2844#else /*Honor_FLT_ROUNDS*/
2845 word0(&rv) = Exp_mask;
2846 word1(&rv) = 0;
2847#endif /*Honor_FLT_ROUNDS*/
2848#ifdef SET_INEXACT
2849 /* set overflow bit */
2850 dval(&rv0) = 1e300;
2851 dval(&rv0) *= dval(&rv0);
2852#endif
2853#else /*IEEE_Arith*/
2854 word0(&rv) = Big0;
2855 word1(&rv) = Big1;
2856#endif /*IEEE_Arith*/
2857 range_err:
2858 if (bd0) {
2859 Bfree(bb);
2860 Bfree(bd);
2861 Bfree(bs);
2862 Bfree(bd0);
2863 Bfree(delta);
2864 }
2865#ifndef NO_ERRNO
2866 errno = ERANGE;
2867#endif
2868 goto ret;
2869 }
2870 e1 >>= 4;
2871 for(j = 0; e1 > 1; j++, e1 >>= 1)
2872 if (e1 & 1)
2873 dval(&rv) *= bigtens[j];
2874 /* The last multiplication could overflow. */
2875 word0(&rv) -= P*Exp_msk1;
2876 dval(&rv) *= bigtens[j];
2877 if ((z = word0(&rv) & Exp_mask)
2878 > Exp_msk1*(DBL_MAX_EXP+Bias-P))
2879 goto ovfl;
2880 if (z > Exp_msk1*(DBL_MAX_EXP+Bias-1-P)) {
2881 /* set to largest number */
2882 /* (Can't trust DBL_MAX) */
2883 word0(&rv) = Big0;
2884 word1(&rv) = Big1;
2885 }
2886 else
2887 word0(&rv) += P*Exp_msk1;
2888 }
2889 }
2890 else if (e1 < 0) {
2891 e1 = -e1;
2892 if ((i = e1 & 15))
2893 dval(&rv) /= tens[i];
2894 if (e1 >>= 4) {
2895 if (e1 >= 1 << n_bigtens)
2896 goto undfl;
2897#ifdef Avoid_Underflow
2898 if (e1 & Scale_Bit)
2899 bc.scale = 2*P;
2900 for(j = 0; e1 > 0; j++, e1 >>= 1)
2901 if (e1 & 1)
2902 dval(&rv) *= tinytens[j];
2903 if (bc.scale && (j = 2*P + 1 - ((word0(&rv) & Exp_mask)
2904 >> Exp_shift)) > 0) {
2905 /* scaled rv is denormal; clear j low bits */
2906 if (j >= 32) {
2907 if (j > 54)
2908 goto undfl;
2909 word1(&rv) = 0;
2910 if (j >= 53)
2911 word0(&rv) = (P+2)*Exp_msk1;
2912 else
2913 word0(&rv) &= 0xffffffff << (j-32);
2914 }
2915 else
2916 word1(&rv) &= 0xffffffff << j;
2917 }
2918#else
2919 for(j = 0; e1 > 1; j++, e1 >>= 1)
2920 if (e1 & 1)
2921 dval(&rv) *= tinytens[j];
2922 /* The last multiplication could underflow. */
2923 dval(&rv0) = dval(&rv);
2924 dval(&rv) *= tinytens[j];
2925 if (!dval(&rv)) {
2926 dval(&rv) = 2.*dval(&rv0);
2927 dval(&rv) *= tinytens[j];
2928#endif
2929 if (!dval(&rv)) {
2930 undfl:
2931 dval(&rv) = 0.;
2932 goto range_err;
2933 }
2934#ifndef Avoid_Underflow
2935 word0(&rv) = Tiny0;
2936 word1(&rv) = Tiny1;
2937 /* The refinement below will clean
2938 * this approximation up.
2939 */
2940 }
2941#endif
2942 }
2943 }
2944
2945 /* Now the hard part -- adjusting rv to the correct value.*/
2946
2947 /* Put digits into bd: true value = bd * 10^e */
2948
2949 bc.nd = nd - nz1;
2950#ifndef NO_STRTOD_BIGCOMP
2951 bc.nd0 = nd0; /* Only needed if nd > strtod_diglim, but done here */
2952 /* to silence an erroneous warning about bc.nd0 */
2953 /* possibly not being initialized. */
2954 if (nd > strtod_diglim) {
2955 /* ASSERT(strtod_diglim >= 18); 18 == one more than the */
2956 /* minimum number of decimal digits to distinguish double values */
2957 /* in IEEE arithmetic. */
2958 i = j = 18;
2959 if (i > nd0)
2960 j += bc.dplen;
2961 for(;;) {
2962 if (--j < bc.dp1 && j >= bc.dp0)
2963 j = bc.dp0 - 1;
2964 if (s0[j] != '0')
2965 break;
2966 --i;
2967 }
2968 e += nd - i;
2969 nd = i;
2970 if (nd0 > nd)
2971 nd0 = nd;
2972 if (nd < 9) { /* must recompute y */
2973 y = 0;
2974 for(i = 0; i < nd0; ++i)
2975 y = 10*y + s0[i] - '0';
2976 for(j = bc.dp1; i < nd; ++i)
2977 y = 10*y + s0[j++] - '0';
2978 }
2979 }
2980#endif
2981 bd0 = s2b(s0, nd0, nd, y, bc.dplen);
2982
2983 for(;;) {
2984 bd = Balloc(bd0->k);
2985 Bcopy(bd, bd0);
2986 bb = d2b(&rv, &bbe, &bbbits); /* rv = bb * 2^bbe */
2987 bs = i2b(1);
2988
2989 if (e >= 0) {
2990 bb2 = bb5 = 0;
2991 bd2 = bd5 = e;
2992 }
2993 else {
2994 bb2 = bb5 = -e;
2995 bd2 = bd5 = 0;
2996 }
2997 if (bbe >= 0)
2998 bb2 += bbe;
2999 else
3000 bd2 -= bbe;
3001 bs2 = bb2;
3002#ifdef Honor_FLT_ROUNDS
3003 if (bc.rounding != 1)
3004 bs2++;
3005#endif
3006#ifdef Avoid_Underflow
3007 Lsb = LSB;
3008 Lsb1 = 0;
3009 j = bbe - bc.scale;
3010 i = j + bbbits - 1; /* logb(rv) */
3011 j = P + 1 - bbbits;
3012 if (i < Emin) { /* denormal */
3013 i = Emin - i;
3014 j -= i;
3015 if (i < 32)
3016 Lsb <<= i;
3017 else if (i < 52)
3018 Lsb1 = Lsb << (i-32);
3019 else
3020 Lsb1 = Exp_mask;
3021 }
3022#else /*Avoid_Underflow*/
3023#ifdef Sudden_Underflow
3024#ifdef IBM
3025 j = 1 + 4*P - 3 - bbbits + ((bbe + bbbits - 1) & 3);
3026#else
3027 j = P + 1 - bbbits;
3028#endif
3029#else /*Sudden_Underflow*/
3030 j = bbe;
3031 i = j + bbbits - 1; /* logb(rv) */
3032 if (i < Emin) /* denormal */
3033 j += P - Emin;
3034 else
3035 j = P + 1 - bbbits;
3036#endif /*Sudden_Underflow*/
3037#endif /*Avoid_Underflow*/
3038 bb2 += j;
3039 bd2 += j;
3040#ifdef Avoid_Underflow
3041 bd2 += bc.scale;
3042#endif
3043 i = bb2 < bd2 ? bb2 : bd2;
3044 if (i > bs2)
3045 i = bs2;
3046 if (i > 0) {
3047 bb2 -= i;
3048 bd2 -= i;
3049 bs2 -= i;
3050 }
3051 if (bb5 > 0) {
3052 bs = pow5mult(bs, bb5);
3053 bb1 = mult(bs, bb);
3054 Bfree(bb);
3055 bb = bb1;
3056 }
3057 if (bb2 > 0)
3058 bb = lshift(bb, bb2);
3059 if (bd5 > 0)
3060 bd = pow5mult(bd, bd5);
3061 if (bd2 > 0)
3062 bd = lshift(bd, bd2);
3063 if (bs2 > 0)
3064 bs = lshift(bs, bs2);
3065 delta = diff(bb, bd);
3066 bc.dsign = delta->sign;
3067 delta->sign = 0;
3068 i = cmp(delta, bs);
3069#ifndef NO_STRTOD_BIGCOMP /*{*/
3070 if (bc.nd > nd && i <= 0) {
3071 if (bc.dsign) {
3072 /* Must use bigcomp(). */
3073 req_bigcomp = 1;
3074 break;
3075 }
3076#ifdef Honor_FLT_ROUNDS
3077 if (bc.rounding != 1) {
3078 if (i < 0) {
3079 req_bigcomp = 1;
3080 break;
3081 }
3082 }
3083 else
3084#endif
3085 i = -1; /* Discarded digits make delta smaller. */
3086 }
3087#endif /*}*/
3088#ifdef Honor_FLT_ROUNDS /*{*/
3089 if (bc.rounding != 1) {
3090 if (i < 0) {
3091 /* Error is less than an ulp */
3092 if (!delta->x[0] && delta->wds <= 1) {
3093 /* exact */
3094#ifdef SET_INEXACT
3095 bc.inexact = 0;
3096#endif
3097 break;
3098 }
3099 if (bc.rounding) {
3100 if (bc.dsign) {
3101 adj.d = 1.;
3102 goto apply_adj;
3103 }
3104 }
3105 else if (!bc.dsign) {
3106 adj.d = -1.;
3107 if (!word1(&rv)
3108 && !(word0(&rv) & Frac_mask)) {
3109 y = word0(&rv) & Exp_mask;
3110#ifdef Avoid_Underflow
3111 if (!bc.scale || y > 2*P*Exp_msk1)
3112#else
3113 if (y)
3114#endif
3115 {
3116 delta = lshift(delta,Log2P);
3117 if (cmp(delta, bs) <= 0)
3118 adj.d = -0.5;
3119 }
3120 }
3121 apply_adj:
3122#ifdef Avoid_Underflow /*{*/
3123 if (bc.scale && (y = word0(&rv) & Exp_mask)
3124 <= 2*P*Exp_msk1)
3125 word0(&adj) += (2*P+1)*Exp_msk1 - y;
3126#else
3127#ifdef Sudden_Underflow
3128 if ((word0(&rv) & Exp_mask) <=
3129 P*Exp_msk1) {
3130 word0(&rv) += P*Exp_msk1;
3131 dval(&rv) += adj.d*ulp(dval(&rv));
3132 word0(&rv) -= P*Exp_msk1;
3133 }
3134 else
3135#endif /*Sudden_Underflow*/
3136#endif /*Avoid_Underflow}*/
3137 dval(&rv) += adj.d*ulp(&rv);
3138 }
3139 break;
3140 }
3141 adj.d = ratio(delta, bs);
3142 if (adj.d < 1.)
3143 adj.d = 1.;
3144 if (adj.d <= 0x7ffffffe) {
3145 /* adj = rounding ? ceil(adj) : floor(adj); */
3146 y = adj.d;
3147 if (y != adj.d) {
3148 if (!((bc.rounding>>1) ^ bc.dsign))
3149 y++;
3150 adj.d = y;
3151 }
3152 }
3153#ifdef Avoid_Underflow /*{*/
3154 if (bc.scale && (y = word0(&rv) & Exp_mask) <= 2*P*Exp_msk1)
3155 word0(&adj) += (2*P+1)*Exp_msk1 - y;
3156#else
3157#ifdef Sudden_Underflow
3158 if ((word0(&rv) & Exp_mask) <= P*Exp_msk1) {
3159 word0(&rv) += P*Exp_msk1;
3160 adj.d *= ulp(dval(&rv));
3161 if (bc.dsign)
3162 dval(&rv) += adj.d;
3163 else
3164 dval(&rv) -= adj.d;
3165 word0(&rv) -= P*Exp_msk1;
3166 goto cont;
3167 }
3168#endif /*Sudden_Underflow*/
3169#endif /*Avoid_Underflow}*/
3170 adj.d *= ulp(&rv);
3171 if (bc.dsign) {
3172 if (word0(&rv) == Big0 && word1(&rv) == Big1)
3173 goto ovfl;
3174 dval(&rv) += adj.d;
3175 }
3176 else
3177 dval(&rv) -= adj.d;
3178 goto cont;
3179 }
3180#endif /*}Honor_FLT_ROUNDS*/
3181
3182 if (i < 0) {
3183 /* Error is less than half an ulp -- check for
3184 * special case of mantissa a power of two.
3185 */
3186 if (bc.dsign || word1(&rv) || word0(&rv) & Bndry_mask
3187#ifdef IEEE_Arith /*{*/
3188#ifdef Avoid_Underflow
3189 || (word0(&rv) & Exp_mask) <= (2*P+1)*Exp_msk1
3190#else
3191 || (word0(&rv) & Exp_mask) <= Exp_msk1
3192#endif
3193#endif /*}*/
3194 ) {
3195#ifdef SET_INEXACT
3196 if (!delta->x[0] && delta->wds <= 1)
3197 bc.inexact = 0;
3198#endif
3199 break;
3200 }
3201 if (!delta->x[0] && delta->wds <= 1) {
3202 /* exact result */
3203#ifdef SET_INEXACT
3204 bc.inexact = 0;
3205#endif
3206 break;
3207 }
3208 delta = lshift(delta,Log2P);
3209 if (cmp(delta, bs) > 0)
3210 goto drop_down;
3211 break;
3212 }
3213 if (i == 0) {
3214 /* exactly half-way between */
3215 if (bc.dsign) {
3216 if ((word0(&rv) & Bndry_mask1) == Bndry_mask1
3217 && word1(&rv) == (
3218#ifdef Avoid_Underflow
3219 (bc.scale && (y = word0(&rv) & Exp_mask) <= 2*P*Exp_msk1)
3220 ? (0xffffffff & (0xffffffff << (2*P+1-(y>>Exp_shift)))) :
3221#endif
3222 0xffffffff)) {
3223 /*boundary case -- increment exponent*/
3224 if (word0(&rv) == Big0 && word1(&rv) == Big1)
3225 goto ovfl;
3226 word0(&rv) = (word0(&rv) & Exp_mask)
3227 + Exp_msk1
3228#ifdef IBM
3229 | Exp_msk1 >> 4
3230#endif
3231 ;
3232 word1(&rv) = 0;
3233#ifdef Avoid_Underflow
3234 bc.dsign = 0;
3235#endif
3236 break;
3237 }
3238 }
3239 else if (!(word0(&rv) & Bndry_mask) && !word1(&rv)) {
3240 drop_down:
3241 /* boundary case -- decrement exponent */
3242#ifdef Sudden_Underflow /*{{*/
3243 L = word0(&rv) & Exp_mask;
3244#ifdef IBM
3245 if (L < Exp_msk1)
3246#else
3247#ifdef Avoid_Underflow
3248 if (L <= (bc.scale ? (2*P+1)*Exp_msk1 : Exp_msk1))
3249#else
3250 if (L <= Exp_msk1)
3251#endif /*Avoid_Underflow*/
3252#endif /*IBM*/
3253 {
3254 if (bc.nd >nd) {
3255 bc.uflchk = 1;
3256 break;
3257 }
3258 goto undfl;
3259 }
3260 L -= Exp_msk1;
3261#else /*Sudden_Underflow}{*/
3262#ifdef Avoid_Underflow
3263 if (bc.scale) {
3264 L = word0(&rv) & Exp_mask;
3265 if (L <= (2*P+1)*Exp_msk1) {
3266 if (L > (P+2)*Exp_msk1)
3267 /* round even ==> */
3268 /* accept rv */
3269 break;
3270 /* rv = smallest denormal */
3271 if (bc.nd >nd) {
3272 bc.uflchk = 1;
3273 break;
3274 }
3275 goto undfl;
3276 }
3277 }
3278#endif /*Avoid_Underflow*/
3279 L = (word0(&rv) & Exp_mask) - Exp_msk1;
3280#endif /*Sudden_Underflow}}*/
3281 word0(&rv) = L | Bndry_mask1;
3282 word1(&rv) = 0xffffffff;
3283#ifdef IBM
3284 goto cont;
3285#else
3286#ifndef NO_STRTOD_BIGCOMP
3287 if (bc.nd > nd)
3288 goto cont;
3289#endif
3290 break;
3291#endif
3292 }
3293#ifndef ROUND_BIASED
3294#ifdef Avoid_Underflow
3295 if (Lsb1) {
3296 if (!(word0(&rv) & Lsb1))
3297 break;
3298 }
3299 else if (!(word1(&rv) & Lsb))
3300 break;
3301#else
3302 if (!(word1(&rv) & LSB))
3303 break;
3304#endif
3305#endif
3306 if (bc.dsign)
3307#ifdef Avoid_Underflow
3308 dval(&rv) += sulp(&rv, &bc);
3309#else
3310 dval(&rv) += ulp(&rv);
3311#endif
3312#ifndef ROUND_BIASED
3313 else {
3314#ifdef Avoid_Underflow
3315 dval(&rv) -= sulp(&rv, &bc);
3316#else
3317 dval(&rv) -= ulp(&rv);
3318#endif
3319#ifndef Sudden_Underflow
3320 if (!dval(&rv)) {
3321 if (bc.nd >nd) {
3322 bc.uflchk = 1;
3323 break;
3324 }
3325 goto undfl;
3326 }
3327#endif
3328 }
3329#ifdef Avoid_Underflow
3330 bc.dsign = 1 - bc.dsign;
3331#endif
3332#endif
3333 break;
3334 }
3335 if ((aadj = ratio(delta, bs)) <= 2.) {
3336 if (bc.dsign)
3337 aadj = aadj1 = 1.;
3338 else if (word1(&rv) || word0(&rv) & Bndry_mask) {
3339#ifndef Sudden_Underflow
3340 if (word1(&rv) == Tiny1 && !word0(&rv)) {
3341 if (bc.nd >nd) {
3342 bc.uflchk = 1;
3343 break;
3344 }
3345 goto undfl;
3346 }
3347#endif
3348 aadj = 1.;
3349 aadj1 = -1.;
3350 }
3351 else {
3352 /* special case -- power of FLT_RADIX to be */
3353 /* rounded down... */
3354
3355 if (aadj < 2./FLT_RADIX)
3356 aadj = 1./FLT_RADIX;
3357 else
3358 aadj *= 0.5;
3359 aadj1 = -aadj;
3360 }
3361 }
3362 else {
3363 aadj *= 0.5;
3364 aadj1 = bc.dsign ? aadj : -aadj;
3365#ifdef Check_FLT_ROUNDS
3366 switch(bc.rounding) {
3367 case 2: /* towards +infinity */
3368 aadj1 -= 0.5;
3369 break;
3370 case 0: /* towards 0 */
3371 case 3: /* towards -infinity */
3372 aadj1 += 0.5;
3373 }
3374#else
3375 if (Flt_Rounds == 0)
3376 aadj1 += 0.5;
3377#endif /*Check_FLT_ROUNDS*/
3378 }
3379 y = word0(&rv) & Exp_mask;
3380
3381 /* Check for overflow */
3382
3383 if (y == Exp_msk1*(DBL_MAX_EXP+Bias-1)) {
3384 dval(&rv0) = dval(&rv);
3385 word0(&rv) -= P*Exp_msk1;
3386 adj.d = aadj1 * ulp(&rv);
3387 dval(&rv) += adj.d;
3388 if ((word0(&rv) & Exp_mask) >=
3389 Exp_msk1*(DBL_MAX_EXP+Bias-P)) {
3390 if (word0(&rv0) == Big0 && word1(&rv0) == Big1)
3391 goto ovfl;
3392 word0(&rv) = Big0;
3393 word1(&rv) = Big1;
3394 goto cont;
3395 }
3396 else
3397 word0(&rv) += P*Exp_msk1;
3398 }
3399 else {
3400#ifdef Avoid_Underflow
3401 if (bc.scale && y <= 2*P*Exp_msk1) {
3402 if (aadj <= 0x7fffffff) {
3403 if ((z = aadj) <= 0)
3404 z = 1;
3405 aadj = z;
3406 aadj1 = bc.dsign ? aadj : -aadj;
3407 }
3408 dval(&aadj2) = aadj1;
3409 word0(&aadj2) += (2*P+1)*Exp_msk1 - y;
3410 aadj1 = dval(&aadj2);
3411 adj.d = aadj1 * ulp(&rv);
3412 dval(&rv) += adj.d;
3413 if (rv.d == 0.)
3414#ifdef NO_STRTOD_BIGCOMP
3415 goto undfl;
3416#else
3417 {
3418 req_bigcomp = 1;
3419 break;
3420 }
3421#endif
3422 }
3423 else {
3424 adj.d = aadj1 * ulp(&rv);
3425 dval(&rv) += adj.d;
3426 }
3427#else
3428#ifdef Sudden_Underflow
3429 if ((word0(&rv) & Exp_mask) <= P*Exp_msk1) {
3430 dval(&rv0) = dval(&rv);
3431 word0(&rv) += P*Exp_msk1;
3432 adj.d = aadj1 * ulp(&rv);
3433 dval(&rv) += adj.d;
3434#ifdef IBM
3435 if ((word0(&rv) & Exp_mask) < P*Exp_msk1)
3436#else
3437 if ((word0(&rv) & Exp_mask) <= P*Exp_msk1)
3438#endif
3439 {
3440 if (word0(&rv0) == Tiny0
3441 && word1(&rv0) == Tiny1) {
3442 if (bc.nd >nd) {
3443 bc.uflchk = 1;
3444 break;
3445 }
3446 goto undfl;
3447 }
3448 word0(&rv) = Tiny0;
3449 word1(&rv) = Tiny1;
3450 goto cont;
3451 }
3452 else
3453 word0(&rv) -= P*Exp_msk1;
3454 }
3455 else {
3456 adj.d = aadj1 * ulp(&rv);
3457 dval(&rv) += adj.d;
3458 }
3459#else /*Sudden_Underflow*/
3460 /* Compute adj so that the IEEE rounding rules will
3461 * correctly round rv + adj in some half-way cases.
3462 * If rv * ulp(rv) is denormalized (i.e.,
3463 * y <= (P-1)*Exp_msk1), we must adjust aadj to avoid
3464 * trouble from bits lost to denormalization;
3465 * example: 1.2e-307 .
3466 */
3467 if (y <= (P-1)*Exp_msk1 && aadj > 1.) {
3468 aadj1 = (double)(int)(aadj + 0.5);
3469 if (!bc.dsign)
3470 aadj1 = -aadj1;
3471 }
3472 adj.d = aadj1 * ulp(&rv);
3473 dval(&rv) += adj.d;
3474#endif /*Sudden_Underflow*/
3475#endif /*Avoid_Underflow*/
3476 }
3477 z = word0(&rv) & Exp_mask;
3478#ifndef SET_INEXACT
3479 if (bc.nd == nd) {
3480#ifdef Avoid_Underflow
3481 if (!bc.scale)
3482#endif
3483 if (y == z) {
3484 /* Can we stop now? */
3485 L = (Long)aadj;
3486 aadj -= L;
3487 /* The tolerances below are conservative. */
3488 if (bc.dsign || word1(&rv) || word0(&rv) & Bndry_mask) {
3489 if (aadj < .4999999 || aadj > .5000001)
3490 break;
3491 }
3492 else if (aadj < .4999999/FLT_RADIX)
3493 break;
3494 }
3495 }
3496#endif
3497 cont:
3498 Bfree(bb);
3499 Bfree(bd);
3500 Bfree(bs);
3501 Bfree(delta);
3502 }
3503 Bfree(bb);
3504 Bfree(bd);
3505 Bfree(bs);
3506 Bfree(bd0);
3507 Bfree(delta);
3508#ifndef NO_STRTOD_BIGCOMP
3509 if (req_bigcomp) {
3510 bd0 = 0;
3511 bc.e0 += nz1;
3512 bigcomp(&rv, s0, &bc);
3513 y = word0(&rv) & Exp_mask;
3514 if (y == Exp_mask)
3515 goto ovfl;
3516 if (y == 0 && rv.d == 0.)
3517 goto undfl;
3518 }
3519#endif
3520#ifdef SET_INEXACT
3521 if (bc.inexact) {
3522 if (!oldinexact) {
3523 word0(&rv0) = Exp_1 + (70 << Exp_shift);
3524 word1(&rv0) = 0;
3525 dval(&rv0) += 1.;
3526 }
3527 }
3528 else if (!oldinexact)
3529 clear_inexact();
3530#endif
3531#ifdef Avoid_Underflow
3532 if (bc.scale) {
3533 word0(&rv0) = Exp_1 - 2*P*Exp_msk1;
3534 word1(&rv0) = 0;
3535 dval(&rv) *= dval(&rv0);
3536#ifndef NO_ERRNO
3537 /* try to avoid the bug of testing an 8087 register value */
3538#ifdef IEEE_Arith
3539 if (!(word0(&rv) & Exp_mask))
3540#else
3541 if (word0(&rv) == 0 && word1(&rv) == 0)
3542#endif
3543 errno = ERANGE;
3544#endif
3545 }
3546#endif /* Avoid_Underflow */
3547#ifdef SET_INEXACT
3548 if (bc.inexact && !(word0(&rv) & Exp_mask)) {
3549 /* set underflow bit */
3550 dval(&rv0) = 1e-300;
3551 dval(&rv0) *= dval(&rv0);
3552 }
3553#endif
3554 ret:
3555 if (se)
3556 *se = (char *)s;
3557 return sign ? -dval(&rv) : dval(&rv);
3558 }
rounded_product
#define rounded_product(a, b)
Definition dtoa.c:479
Tiny0
#define Tiny0
Definition dtoa.c:454
rounded_quotient
#define rounded_quotient(a, b)
Definition dtoa.c:480
Tiny1
#define Tiny1
Definition dtoa.c:455
gethex
void gethex(CONST char **sp, U *rvp, int rounding, int sign)
Definition dtoa.c:1762
LSB
#define LSB
Definition dtoa.c:451
strtod_diglim
#define strtod_diglim
Definition dtoa.c:324
Bndry_mask1
#define Bndry_mask1
Definition dtoa.c:450
fc::y
uint64_t y
Definition sha3.cpp:34
sysio::chain::resource_limits::ratio
impl::ratio< uint64_t > ratio
Definition resource_limits.hpp:32
BCinfo
Definition dtoa.c:492
BCinfo::e0
int e0
Definition dtoa.c:492
BCinfo::dp0
int dp0
Definition dtoa.c:492
BCinfo::scale
int scale
Definition dtoa.c:492
BCinfo::uflchk
int uflchk
Definition dtoa.c:492
BCinfo::dplen
int dplen
Definition dtoa.c:492
BCinfo::nd0
int nd0
Definition dtoa.c:492
BCinfo::dp1
int dp1
Definition dtoa.c:492
BCinfo::nd
int nd
Definition dtoa.c:492
BCinfo::inexact
int inexact
Definition dtoa.c:492
BCinfo::dsign
int dsign
Definition dtoa.c:492
BCinfo::rounding
int rounding
Definition dtoa.c:492
rv
CK_RV rv
Definition yubihsm_pkcs11.c:569
Here is the call graph for this function:

Variable Documentation

◆ IEEE_8087

Exactly one of IEEE_8087

Definition at line 303 of file dtoa.c.

◆ IEEE_MC68k

Exactly one of IEEE_MC68k

Definition at line 303 of file dtoa.c.

◆ VAX

Exactly one of VAX

Definition at line 303 of file dtoa.c.