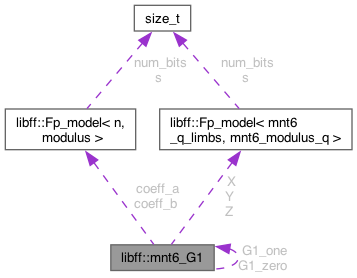
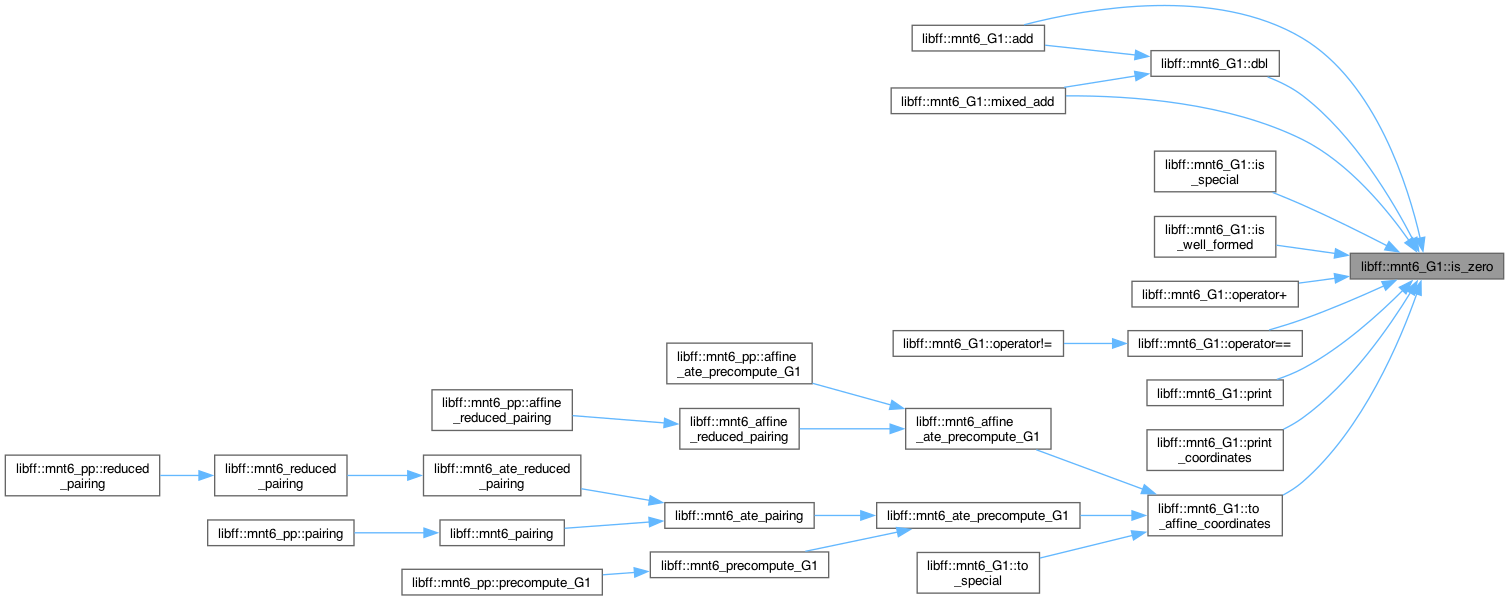
#include <mnt6_g1.hpp>
Definition at line 26 of file mnt6_g1.hpp.
◆ base_field
◆ scalar_field
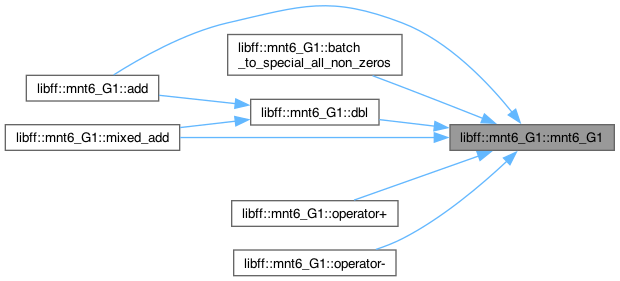
◆ mnt6_G1() [1/3]
| libff::mnt6_G1::mnt6_G1 |
( |
| ) |
|
◆ mnt6_G1() [2/3]
Definition at line 47 of file mnt6_g1.hpp.
static Fp_model< n, modulus > one()
◆ mnt6_G1() [3/3]
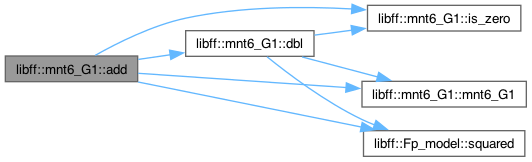
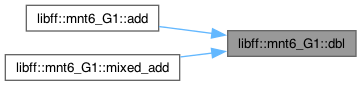
◆ add()
Definition at line 224 of file mnt6_g1.cpp.
225{
226
228 {
230 }
231
233 {
234 return (*this);
235 }
236
237
238
239
240
241 if (this->operator==(other))
242 {
244 }
245
246#ifdef PROFILE_OP_COUNTS
247 this->add_cnt++;
248#endif
249
250
251
263 const mnt6_Fq Y3 = u * (
R-
A) - vvv * Y1Z2;
265
267}
Fp_model< mnt6_q_limbs, mnt6_modulus_q > mnt6_Fq
◆ base_field_char()
Definition at line 77 of file mnt6_g1.hpp.
static bigint< n > field_char()
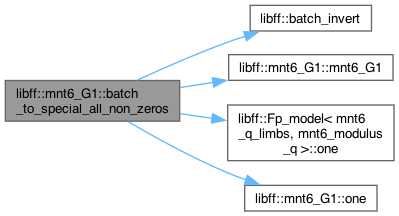
◆ batch_to_special_all_non_zeros()
| void libff::mnt6_G1::batch_to_special_all_non_zeros |
( |
std::vector< mnt6_G1 > & | vec | ) |
|
|
static |
Definition at line 488 of file mnt6_g1.cpp.
489{
490 std::vector<mnt6_Fq> Z_vec;
491 Z_vec.reserve(vec.size());
492
493 for (auto &el: vec)
494 {
495 Z_vec.emplace_back(el.Z);
496 }
498
500
501 for (size_t i = 0; i < vec.size(); ++i)
502 {
503 vec[i] =
mnt6_G1(vec[i].
X * Z_vec[i], vec[i].
Y * Z_vec[i],
one);
504 }
505}
void batch_invert(std::vector< FieldT > &vec)
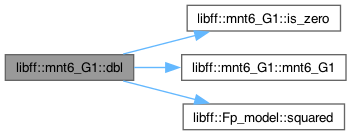
◆ dbl()
| mnt6_G1 libff::mnt6_G1::dbl |
( |
| ) |
const |
Definition at line 319 of file mnt6_g1.cpp.
320{
321#ifdef PROFILE_OP_COUNTS
322 this->dbl_cnt++;
323#endif
325 {
326 return (*this);
327 }
328 else
329 {
330
331
332
333 const mnt6_Fq XX = (this->
X).squared();
334 const mnt6_Fq ZZ = (this->
Z).squared();
336 const mnt6_Fq Y1Z1 = (this->
Y) * (this->
Z);
342 const mnt6_Fq B = ((this->
X)+
R).squared()-XX-RR;
345 const mnt6_Fq Y3 = w * (
B-h)-(RR+RR);
347
349 }
350}
static const Segment ss(Segment::ss)
◆ is_special()
| bool libff::mnt6_G1::is_special |
( |
| ) |
const |
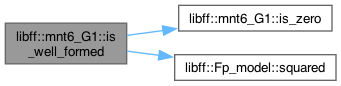
◆ is_well_formed()
| bool libff::mnt6_G1::is_well_formed |
( |
| ) |
const |
Definition at line 352 of file mnt6_g1.cpp.
353{
355 {
356 return true;
357 }
358 else
359 {
360
361
362
363
364
365
366
367
368
369
370 const mnt6_Fq X2 = this->
X.squared();
373
375 }
376}
◆ is_zero()
| bool libff::mnt6_G1::is_zero |
( |
| ) |
const |
Definition at line 99 of file mnt6_g1.cpp.
100{
101 return (this->
X.is_zero() && this->Z.is_zero());
102}
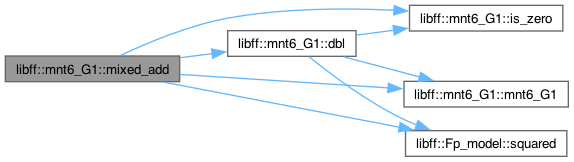
◆ mixed_add()
Definition at line 269 of file mnt6_g1.cpp.
270{
271#ifdef PROFILE_OP_COUNTS
272 this->add_cnt++;
273#endif
274
275
276
277
279 {
281 }
282
284 {
285 return (*this);
286 }
287
288#ifdef DEBUG
289 assert(
other.is_special());
290#endif
291
294
295
296
299
300 if (X1Z2 == X2Z1 && Y1Z2 == Y2Z1)
301 {
303 }
304
315
317}
◆ one()
◆ operator!=()
| bool libff::mnt6_G1::operator!= |
( |
const mnt6_G1 & | other | ) |
const |
Definition at line 133 of file mnt6_g1.cpp.
134{
136}
bool operator==(const mnt6_G1 &other) const
◆ operator+()
Definition at line 138 of file mnt6_g1.cpp.
139{
140
142 {
144 }
145
147 {
148 return *this;
149 }
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
170
171
172
175
176 if (X1Z2 == X2Z1 && Y1Z2 == Y2Z1)
177 {
178
179 const mnt6_Fq XX = (this->
X).squared();
180 const mnt6_Fq ZZ = (this->
Z).squared();
182 const mnt6_Fq Y1Z1 = (this->
Y) * (this->
Z);
188 const mnt6_Fq B = ((this->
X)+
R).squared()-XX-RR;
191 const mnt6_Fq Y3 = w * (
B-h)-(RR+RR);
193
195 }
196
197
207 const mnt6_Fq Y3 = u * (
R-
A) - vvv * Y1Z2;
209
211}
◆ operator-() [1/2]
| mnt6_G1 libff::mnt6_G1::operator- |
( |
| ) |
const |
◆ operator-() [2/2]
◆ operator==()
| bool libff::mnt6_G1::operator== |
( |
const mnt6_G1 & | other | ) |
const |
Definition at line 104 of file mnt6_g1.cpp.
105{
107 {
108 return other.is_zero();
109 }
110
112 {
113 return false;
114 }
115
116
117
118
120 {
121 return false;
122 }
123
124
126 {
127 return false;
128 }
129
130 return true;
131}
◆ order()
◆ print()
| void libff::mnt6_G1::print |
( |
| ) |
const |
Definition at line 41 of file mnt6_g1.cpp.
42{
44 {
46 }
47 else
48 {
50 copy.to_affine_coordinates();
51 gmp_printf("(%Nd , %Nd)\n",
54 }
55}
static const mp_size_t num_limbs
LOGGING_API void printf(Category category, const char *format,...)
void copy(const path &from, const path &to)
◆ print_coordinates()
| void libff::mnt6_G1::print_coordinates |
( |
| ) |
const |
Definition at line 57 of file mnt6_g1.cpp.
58{
60 {
62 }
63 else
64 {
65 gmp_printf("(%Nd : %Nd : %Nd)\n",
69 }
70}
◆ random_element()
| mnt6_G1 libff::mnt6_G1::random_element |
( |
| ) |
|
|
static |
Definition at line 388 of file mnt6_g1.cpp.
389{
391}
static Fp_model< n, modulus > random_element()
◆ size_in_bits()
| static size_t libff::mnt6_G1::size_in_bits |
( |
| ) |
|
|
inlinestatic |
Definition at line 76 of file mnt6_g1.hpp.
static size_t size_in_bits()
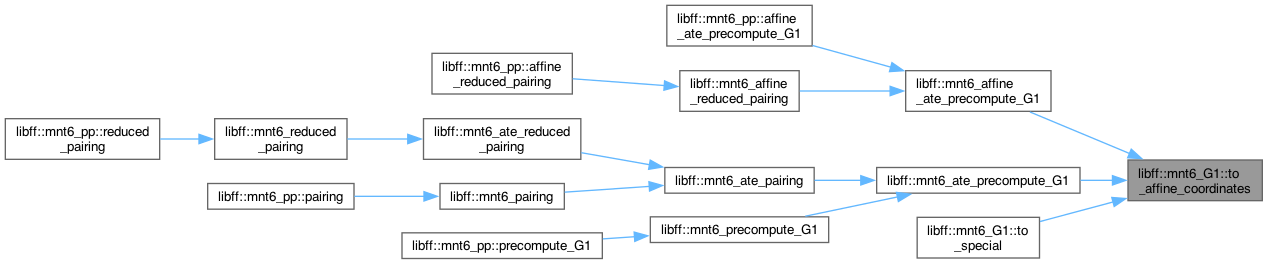
◆ to_affine_coordinates()
| void libff::mnt6_G1::to_affine_coordinates |
( |
| ) |
|
Definition at line 72 of file mnt6_g1.cpp.
73{
75 {
79 }
80 else
81 {
83 this->
X = this->
X * Z_inv;
84 this->
Y = this->
Y * Z_inv;
86 }
87}
static Fp_model< n, modulus > zero()
◆ to_special()
| void libff::mnt6_G1::to_special |
( |
| ) |
|
Definition at line 89 of file mnt6_g1.cpp.
90{
92}
void to_affine_coordinates()
◆ zero()
◆ operator<<
| std::ostream & operator<< |
( |
std::ostream & | out, |
|
|
const mnt6_G1 & | g ) |
|
friend |
Definition at line 393 of file mnt6_g1.cpp.
394{
396 copy.to_affine_coordinates();
397
399#ifdef NO_PT_COMPRESSION
401#else
402
404#endif
405
406 return out;
407}
◆ operator>>
| std::istream & operator>> |
( |
std::istream & | in, |
|
|
mnt6_G1 & | g ) |
|
friend |
Definition at line 409 of file mnt6_g1.cpp.
410{
413
414#ifdef NO_PT_COMPRESSION
417#else
421
422 unsigned char Y_lsb;
423 in >> tX;
425 in.read((char*)&Y_lsb, 1);
426 Y_lsb -= '0';
427
428
430 {
434
435 if ((tY.as_bigint().data[0] & 1) != Y_lsb)
436 {
437 tY = -tY;
438 }
439 }
440#endif
441
443 {
444 g.X = tX;
445 g.Y = tY;
447 }
448 else
449 {
451 }
452
453 return in;
454}
void consume_OUTPUT_SEPARATOR(std::istream &in)
◆ coeff_a
◆ coeff_b
◆ fixed_base_exp_window_table
| std::vector< size_t > libff::mnt6_G1::fixed_base_exp_window_table |
|
static |
◆ G1_one
| mnt6_G1 libff::mnt6_G1::G1_one = {} |
|
static |
◆ G1_zero
| mnt6_G1 libff::mnt6_G1::G1_zero = {} |
|
static |
◆ initialized
| bool libff::mnt6_G1::initialized = false |
|
static |
◆ wnaf_window_table
| std::vector< size_t > libff::mnt6_G1::wnaf_window_table |
|
static |
The documentation for this class was generated from the following files:
- libraries/fc/libraries/ff/libff/algebra/curves/mnt/mnt6/mnt6_g1.hpp
- libraries/fc/libraries/ff/libff/algebra/curves/mnt/mnt6/mnt6_g1.cpp